What is the difference between natural, fundamental, resonant, and forced frequencies?

Question

I'm just overall slightly confused on their exact definitions, as they get thrown around a lot.

Answer 1

Starting with a simple point mass and ideal spring system with no air resistance.
If the mass is displaced from its equilibrium position and released the mass will oscillate at its natural frequency of oscillation - frequency of free oscillations without damping.
There is a complication if the system is damped ie the system loses energy with time eg due to fluid friction.
After the system is displaced it will again oscillate but at a lower frequency as compared with the undamped case - frequency of free oscillations with damping.
The difference between the two frequencies is small if the amount of damping is small.
You can investigate the variation of frequency with damping using this simulation but note that this simulation only seems to work with Internet Explorer and by allowing Java to run the simulation.

---

You can think of a vibration string fixed at both ends as many masses linked by many springs.
That being the case the string has many natural frequencies of free vibration.
Plucking the string in the middle and waiting results in the string oscillating at a natural frequency which is lower than all the rest and this is called the fundamental.
Touch the string lightly at its centre and pluck the string midway between the centre and an end and the string will undergo free oscillations but at a higher frequency.

---

Going back to the simple spring-mass (driveN) system and have it coupled to a system (driveR) which is going to force the driveN system to oscillate.
When first excited by the driveR the motion of the driveN system will be the sum of oscillations at the natural frequency of the driveN system (transient) and oscillations at the frequency of the driveR (steady state).
With damping present the transient oscillation will decay and the system will oscillate at the frequency of the driveR - you could called these the frequency of forced oscillation.
At a particular frequency of the driveR the response of the driveN system is a maximum and this frequency is called the resonance frequency.
This is a simulation which you could use to investigate the dying out of the transients and the steady state behaviour.

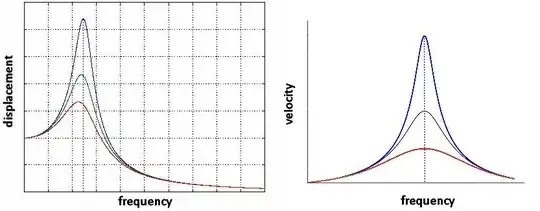
For light damping the amplitude of oscillations of the driveN system are a maximum when the frequency of the driveR is equal to the natural frequency of the driveN system and this condition is called (displacement) resonance.
As the damping increases the frequency at which the amplitude of the driveN is a maximum decreases ie the resonance frequency has decreased.

---

To complicate matters you can consider the what the frequency of the driveR is when the amplitude of the speed of the driveN is a maximum.
This is called velocity resonance and the resonance frequency is the natural frequency of the driveN system.

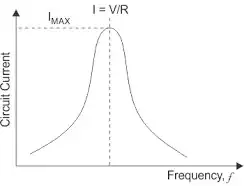
The reason for mentioning this is that for electrical circuits when resonance is considered for, say, an LCR series circuit it is often current (voltage across resistor) resonance which is considered and that corresponds to velocity resonance in the mechanical case with the resonance frequency not dependent on the amount of damping (resistance) in the circuit.

Because of this difference you might notice that that the shape of resonance / forced oscillation graphs for mechanical systems are different from those for electrical systems except when the damping is very light.

Answer 2

natural, fundamental, and resonant frequencies refer to the same thing. Forced frequency is, at least from the standpoint of dynamical systems control theory, whatever the driving frequency is that happens to be applied to the system. This may be defined differently in different fields.