3

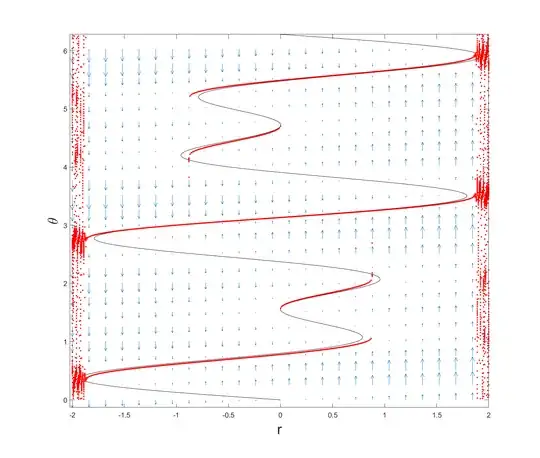
I've been reading about the vector field on a circle, and how it's used to describe stable points for periodic motion. I have also read about how bifurcation diagrams describe changes in positions of visible stable points of a system with respect to a certain parameter.

Let's consider a system described by the vector field on a circle described by $$\dot{\theta}=\sin\theta + r.$$ This system should be valid because the value of $\dot{\theta}$ is the same for all equivalent values of theta (i.e. $\theta=0$ and $\theta=2\pi$ yield the same $\dot{\theta}$). Clearly, the stable point is going to be $\arcsin(-\theta)$ and it is unique.

I tried to think about the bifurcation diagram for this and I decided that it should be something like this:

1

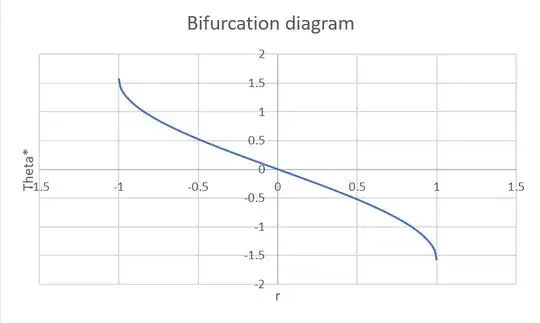
That doesn't seem too meaningful; it's as simple as plotting the solutions for $\dot{\theta}=0$.

I've considered a few other kinds of real, intuitive periodic systems: simple pendulums, damped pendulums, and double pendulums, but I can't find any situations where you'd get something like a pitchfork/saddle-node bifurcation.

Are there any periodic systems which have more meaningful bifurcation diagrams? By 'meaningful', I'm referring to diagrams which express stuff which isn't obvious through elementary transformation of an equation. For example, I view the above diagram as 'kind-of meaningless' because it's really just $r=\arcsin(-\theta)$.

Alternatively, is there a special significance of bifurcation diagrams for such systems?

Vincent Thacker
  • 15,416

2 Answers2

1

I'm not sure you will like this answer, because it involves a large system of phase oscillators, instead of a single one. (I call "phase oscillators" these systems described by a single variable living on $[0, 2\pi)$ with periodic boundary conditions, such as the ones you describe.

A very interesting system is the Kuramoto model. It is a system of $N$ phase oscillators described by the following equation: $$ \dot\theta_i = \omega_i + \frac{K}{N}\sum_{j=1}^N \sin(\theta_i - \theta_j).$$

Here, $K$ is a coupling constant, and $\omega_i$ is the natural frequency of each oscillator. These are usually assumed to be drawn from a known distribution.

The Kuramoto model does indeed exhibit a phase transition between a synchronised state and a non-synchronised state. Define a complex order parameter as $$ re^{i\psi} = \frac{1}{N} \sum_{j=1}^N e^{i\theta_j}$$ and you can see $r$ is zero when there is no synchronisation, and is one when the thetas are all equal. From this, you can prove (it's easy) that the first equation can be rewritten as $$ \dot\theta_i = \omega_i + Kr \sin(\psi - \theta_j).$$

Now, I leave it to you to prove that this equation has a bifurcation point between disorder ($r=0$) and synchronisation ($r>0$). Have fun!

Martino
  • 3,350
1

The bifurcation diagram you give is pretty meaningful. For $r<-1$ there is no stable point, for $-1\leq r\leq 1$ there is one, and for $r>1$ there is none: this tells us important things about the dynamics, even if it does not look fancy!

To get more involved diagrams, consider more nonlinear functions. For example, what about $\theta' = \sin(5\theta)+\sin(3\theta)+r$? Here there is a saddle-node bifurcation between $0.8<r<0.9$ where we go from 4 attractive fixed points to two. In fact, as you go from $r=-2$ to $r=2$ you get several bifurcations.

Why? Because the number of solutions to $\theta'=0$ changes. If you plot $f(\theta)=\sin(5\theta)+\sin(3\theta)+r$ you will see not just that the zeros change when $r$ increases, but also that there are unstable fixed points where $f(\theta)=0$ but $f'(\theta)>0$, like for $\theta=0$. Add some extra nonlinearity like $(1/10)\sin(2\theta)$ and the saddle-node bifurcations happen in sequence rather than simultaneously.

Bifurcation diagram Simple bifurcation plot of $\theta'=\sin(5\theta)+\sin(3\theta)+\sin(2\theta)/10+r$. Black line denotes the locus of critical points $\theta'=0$, blue arrows indicate magnitude and direction of $\theta'$. Red dots are numerical solutions of the differential equation after a given time, $\theta(T)$, their starting points equidistantly distributed around the circle. Note the intermittency for $r<-1.9$ and $r>1.9$ where there are no stable points but solutions spend much time in the vicinity since $|\theta'|$ is small. Inaccuracies in the solution method makes the point slip from the critical locus near the saddle-node bifurcations.

The fact that the system is easy to analyse is a virtue, not a vice.

Anders Sandberg
  • 34,657