How can pressure act in both the up and down direction?

Question

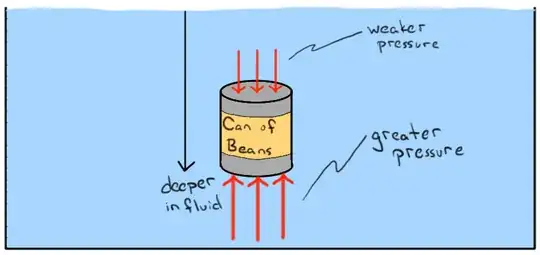
It says in my textbook that pressure is a vector. So how does it act both in the up and down direction in the same body of water as seen in this image?

Answer 1

The pressure is not a vector. It is the force per unit area, and the force acts perpendicularly to the area. The pressure in fluid is due the motion of the molecules. The force arises because of momentum exchanges. Since the molecules are in motion randomly in every direction there is an exchange of momentum with different planes. The momentum transfer occurs in a direction perpendicular to the plane. It is therefore acting in every direction at every point in a fluid.

When gravity is considered, the weight of the fluid provides the force. When acts on the top and bottom surfaces it provides a pressure. So between two depths there is a difference in the weight of the fluid. Imagine replacing the can of beans with a circular cylinder of the same size and let it be a volume of fluid of mass $m$ and cross-sectional area, i.e. the area of the flat circular flace of the can) be $A$ and height $h$ we find that in equilibrium the forces sum to zero to give

$$P_b A - P_t A = mg\,,$$ where $P_{b}$ is the pressure at the bottom of the mass of fluid (the bottom of the can in this case) and $P_{t}$ is the pressure at the top of the mass of fluid (the top of the can in your question.)

For a fluid of constant density $\rho$ the mass is given by $m=\rho V$. Writing $V=Ah$ we obtain

$$P_bA-P_tA = \rho Ahg\,.$$

Dividing across by the cross-sectional area, which is the area of the circular face of the can of beans in your question, we get

$$P_b - P_t = \rho gh\,.$$

See Cutnell & Johnson's "Essentials of Physics."

Edit: Upon reading further, I discovered that pressure in a fluid is also due to the interatomic/intermolecular forces. There are molecules all around a single individual molecule and they are in motion and exerting forces on each other. This explains why the pressure acts in every direction in a liquid. Thus pressure is not a vector. The microscopic explanation of pressure in a liquid is discussed in the answer to the Physics StackExchange question Microscopic interpretation of pressure in liquids

Answer 2

Pressure isn't really a vector, but it's related to a lot of vector quantities. Pressure* is actually a scalar (i.e. it's "just a number;" it has a magnitude, but not a direction, at any point in space); specifically, it's a scalar that is derived from a more complicated object called the stress tensor which contains information about the forces at every point in space in a material. Since forces are vectors, and forces are the inputs for the stress tensor which eventually gives rise to the pressure, one might be able to say that pressure is derived from vector quantities, which is basically what your diagram shows.

Another way in which pressure is related to vector quantities is when calculating the buoyant force. Doing such a calculation requires that you take the gradient of the pressure; the gradient is an operation that converts a scalar function into a vector function. Specifically, it describes how much, and in what direction, the pressure changes as you move through a material. So it's also true that the pressure gradient is a vector, which is basically what @zeta-band is getting at in the comments.

*Technically, what I'm referring to here is static pressure, as opposed to dynamic pressure, because that's what your diagram appears to refer to. If your textbook actually meant dynamic pressure (i.e. the kinetic energy of moving fluid), then that's still a scalar, but there's a closely related quantity, the momentum density, which is a vector.

Answer 3

Pressure is an ambiguous word. I can apply pressure to a thumbtack, and that's a force, and is a vector. But, we also speak of air pressure, or hydraulic pressure, referring to a scalar quantity called hydrostatic pressure. The difference is, hydrostatic pressure is quantified as force per unit area and represents the fact that any small bit of a fluid can push its way out of a container, in any direction.

Squeeze a poly bottle of mustard, and the sideways force of your hand pressurizes the interior, and it squirts... up, down, or wherever the nozzle points. The force of your hands on the sides of the bottle is vector force (and if you push one-sided, the bottle accelerates), but the pressure of the contained mustard is hydraulic pressure, which can propel the mustard through any opening, in any direction.

The behavior of incompressible fluids (constant volume but no particular shape) makes useful working devices, with the hydraulic pressure as an important variable, but that variable wasn't given a one-word name that distinguishes it from my thumb pressing a thumbtack. And the behavior of compressible fluids (like the air in a tire) is also useful, in a different, spring-like way. It's called pressure, too, or hydrostatic pressure (but usually not hydraulic pressure).

Answer 4

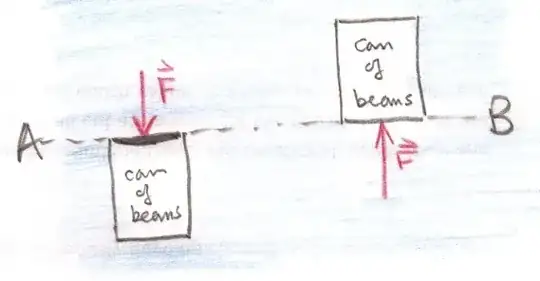
Perhaps this simple example shows you that pressure is not a vector.

In the diagram below the dashed line $AB$ is horizontal and the can is immersed in a fluid.
The pressure at each point along line $AB$ is the same.

Note what happens when the top of the can of beans is placed along line $AB$ and then the bottom of the can is placed along line $AB$.

In both cases the ends of the can experience the same pressure, however, the force which is exerted on the end of the can is reversed.

It is the force $\vec F$ exerted by the fluid which is the vector quantity.

Possibly the confusion arises because pressure is defined as force divided by area $P=\frac FA$ and because the right hand side of the defining equation is a vector $\vec F$ so must be the left hand which is the pressure.

However this is not correct because the force direction is actually related to the orientation of the area; the force is at right angles to the area.

How can this be written as a vector equation which defines pressure?

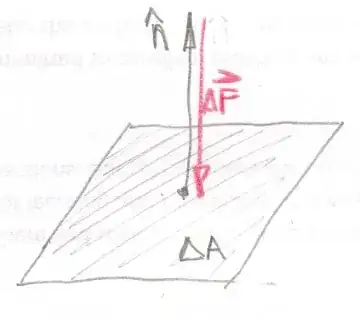
The area is made a vector quantity using the relationship $\Delta \vec A = \Delta A \,\hat n$ where $\Delta A$ is the area and $\hat n$ is a unit vector which is at right angles to the area.
The use of $\Delta$s is to show that even if you have a large surface which is curved that curved surface can be thought of as being made up of many small surfaces which are planar.

Now one can write $\Delta \vec F = - P \, \Delta A \,\hat n$ as the defining vector equation for pressure with the pressure as a scalar.

The minus sign is there because the direction of the normal to the area is opposite to the direction of the force exerted by the fluid.

Converting this to a scalar equation is simple.

$\Delta \vec F = - P \, \Delta A \,\hat n \Rightarrow \Delta F \,(-\hat n) = - P \, \Delta A \,\hat n \Rightarrow \Delta F = P\,\Delta A$