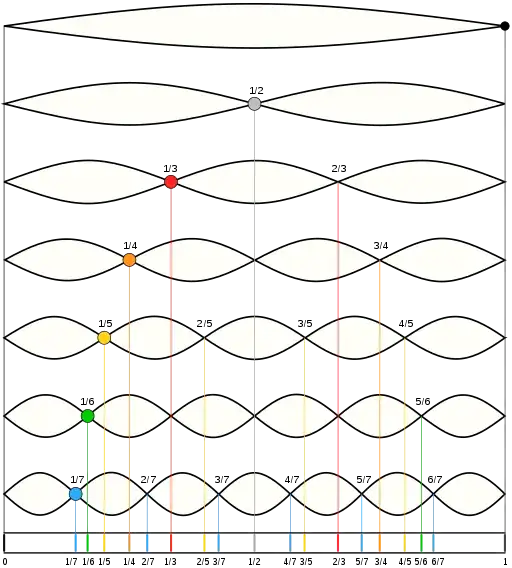
1) Let's imagine we have a string of length $L$ that is fixed at both ends. When we refer to harmonics we are talking about standing waves. Since we are talking about standing waves, we are limited on the allowed wavelengths our standing waves can have. (See picture below)
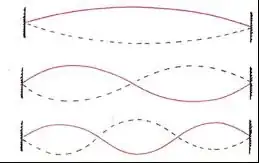
As you can see, the first harmonic has wavelength $\lambda = 2L$, the second has wavelength $\lambda=L$, and the third has $\lambda=\frac 23L$. In general, our allowed harmonics have $\lambda_n=\frac 2nL$, where $n$ is the number of the harmonic.
So what about other properties like wave speed and frequency? Well the speed of a wave in a medium is completely dependent on the properties of the medium and the "tension" the medium is under (which you could argue is a property of the specific medium you are using). For waves on a string, the speed is given by $$v=\sqrt {\frac T\rho}$$, where $T$ is the tension the string is under (which is something that is easily controlled), and $\rho$ is the linear mass density of the string (something that is harder to control if you already have the string made). So as you can see, once you have your string system set up, your speed and allowed wavelengths are pretty much set already.
With all of that in mind, we can now determine what frequencies we need to oscillate one end of the rope at in order to get these harmonics. The speed, wavelength, and frequency of waves are related by $v=f\lambda$, so the frequencies we want are
$$f_n=\frac v\lambda_n=\frac{n}{2L}\sqrt {\frac T\rho}$$
So this is how you "get to your harmonics". You have to oscillate an end of your string at one of these allowed frequencies. Of course, you can change what these frequency values are if you modify things like the length or tension of the string, but once you have the string physically set up, you just need to oscillate the string at the right frequency. (Arguments like these are true for other media and waves, but the forms of the equations will look somewhat different).
2) If you just use the equation from before $v=f\lambda$, you can see that if we double $f$ and half $\lambda$, then $v$ stays the same. You can also argue that the speed will not change since we are not altering any physical properties of the string. Although other things will be different than above since the rope is not fixed at both ends, but you did not ask for details into that, so I will not discuss them either.