Parker Solar Probe top speed

Question

All the news articles say it'll orbit the sun at 430,000 mph. How do they get that? It seems too low. Isn't orbital velocity proportional to $1/\sqrt{r}$? Parker will be 4 million miles above the "surface" of the sun, thus 5 million miles from its center. Earth is about 94 million miles away from the sun's center. Therefore this thing should orbit $(94/5)^2$ times as fast as we do, or about 26 million mph, or so it seems to me.

The big pull that will make the Parker Solar Probe the fastest human-made object. David Freeman, MACH, August 16 2018.

Answer 1

This isn't right:

Isn't orbital velocity proportional to $1/\sqrt{r}$?

For a keplerian elliptical orbit with constant energy, the relation you're looking for is $$ \frac12 mv^2 - \frac{GMm}{r} = E = \mathrm{const}. $$ Orbital velocity is only proportional to $1/\sqrt{r}$ when $E=0$, i.e., for a parabolic orbit. For circular and quasi-circular orbits, the total orbital energy is roughly half the potential energy (in magnitude), so if you leave it out then you'll get some very wrong numbers.

For the Parker Solar Probe's elliptical orbit, the data you've given (a perihelion velocity of $430,000\:\mathrm{mph} = 192\:\mathrm{km/s}$ at a perihelion of $6.9\:\rm Gm$) allows you to calculate the specific orbital energy as \begin{align} \frac Em & = \frac12 v_0^2 - \frac{GM_\odot}{r_0} \\& \approx - 800 \: \rm km^2/s^2 \end{align} and with that you can calculate the aphelion velocity:

• at the true aphelion distance, at the Venus orbital radius of $r_1=108\:\rm Gm$, giving $$ v_1 = \sqrt{2\left(E_0 + \frac{GM_\odot}{r_1}\right)} \approx 29 \:\rm km/s $$
• at a (completely fake!) aphelion at the Earth orbital radius, which produces an aphelion velocity of about $v_2\approx 13\:\rm km/s$.

Here $v_1$ is roughly equal to the Earth's orbital speed (but at a much lower aphelion) whereas $v_2$ (which corresponds to a completely fictional orbit that might not make sense at all) is a good deal slower than that.

Furthermore, it's important to dig a bit into this:

Earth is about 94 million miles away from the sun's center. Therefore this thing should orbit $(94/5)^2$ times as fast as we do.

That presupposes that the probe goes directly to the Sun and then returns to the Earth orbital radius, which is not how the orbit is planned out. Instead, the orbit includes a Venus flyby on the first orbit, which will drastically lower the aphelion and drain the orbital energy; the second aphelion will be at something like 0.9 AU and it only goes down from there, via a series of Venus flybys through the mission which will repeatedly take orbital energy away and lower both the perihelion and the aphelion:

^{Image source}

^{Image source Venus flybys marked as green circles.}

Answer 2

Isn't orbital velocity proportional to $1/\sqrt r$?

As Emilio Pisanty mentioned in his answer, that's the speed of an object on a parabolic trajectory. That requires a fairly high velocity. The orbital speed drops to $1/\sqrt{2r}$ for an object in a circular orbit. The general rule, for all kinds of orbits in the two body problem is given by the vis viva equation, $$v^2 = G(M_1+M_2)\left(\frac2r-\frac1a\right)$$ where $v$ is the relative velocity between the two gravitating objects, $M_1$ and $M_2$ are their masses, $r$ is the distance between the objects, and $a$ is the semi-major axis length of the conic section (circles, ellipses, parabolae, and hyperbolae). Note that the semi-major axis length is infinite for a parabola and negative for a hyperbola. In the case of a tiny mass such as the Parker Space Probe and a large mass such as the Sun, this reduces to $$v^2 = \mu_\odot\left(\frac2r-\frac1a\right)$$ where $\mu_\odot \equiv GM_\odot$ is the Sun's standard gravitational parameter.

The vis viva equation appears so often in orbital mechanics that it's worthwhile remembering it.

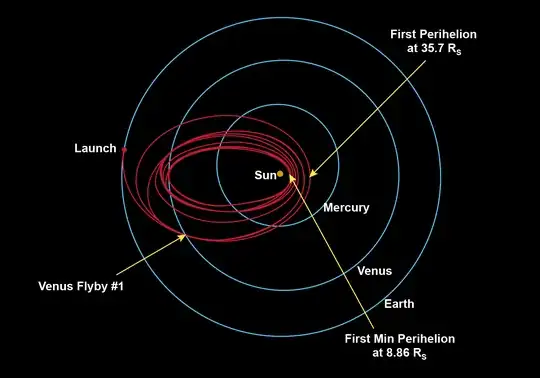
After multiple gravity assists from Venus, the Parker Space Probe's perihelion distance will be h=3.83 million miles above the surface of the Sun, or $r_\odot+h$ from the center of the Sun. It's aphelion distance will be a bit above $R_v$, Venus's orbital radius. The semimajor axis length of the orbit is thus $(R_v+r_s+h)/2$, and the velocity at perihelion is $$v_p = \sqrt{\mu_\odot \left(\frac2{r_\odot+h} - \frac2{R_v+r_\odot+h}\right)} = \sqrt{\frac{2\mu_\odot}{R_v+r_\odot+h}\frac{R_v}{r_\odot+h}}$$

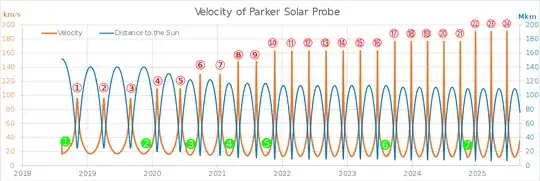
One could go through the tedium of looking up the Sun's radius ($695700\, \text{km}$) and gravitational parameter ($132712440018\,\mathrm{km}^3/\mathrm{s}^2$), Venus's orbital radius ($108208930\,\text{km}$), and converting 3.83 million miles to something sensible ($6164000\,\mathrm{km}$), arrive at an answer of 190.8 km/s with the help of a nice online calculator.

But why bother? The linked online calculator is rather smart. It can do that tedious stuff. Just tell it what you want.