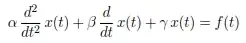0

The equation of linear motion in a given coordinate axis (say $x$) in my text book:

enter image description here

And throughout my mechanics course I never encountered derivative with power higher than 2 in EOM?

Why is it so?

Does additional derivatives put on any restriction in a physical sense which although mathematically constructable but not physically possible? (just like imaginary roots in quadratic equation in certain problems had imaginary or negative roots of time)

EDIT: It turns out that there exist two anser which adresses the problem in terms of lagrangian mechanics

Is there any equivalent explanation from the point of view of Newtonian Dynamics?

user203163
  • 1

1 Answers1

-2

As a rule of thumb anything higher than a second derivative will correspond to something nonlocal.

Think about it this way, I expect that I should be able to solve my equations of motion by only knowing whats going on locally. But If I had to know all the derivatives of my function, then that's enough to construct the function everywhere using the Taylor series which means that I have to know whats going on everywhere.

YankyL
  • 443