What "transformations" did Abrikosov use in 1958 to get the famous $11-2\log{2}$ result in fermi-liquid theory?

Question

How does one obtain the final integral expression in the appendix of Abrikosov and Khalatnikov's 1958 paper: $\ \ \ $ "Concerning a model for a non-ideal fermi gas" $\ \ \ $ ???

Below, in Bold, I will mark the point at which I am stuck.

The paper is freely available from JETP -- http://www.jetp.ac.ru/cgi-bin/dn/e_006_05_0888.pdf

This problem is an important one, as the term "$11-2\log{2}$" appears in many fields of physics, e.g., in Fetter and Walecka "Many Particle Systems", Landau and Lifshitz "Statistical Physics", problems in nuclear physics, problems in neutron star equation of state, density-functional theory, etc. However, the integral is never shown in its details, probably because its original derivation by Huang and Yang (1957) used a very laborious approach, and numerical methods are easier these days. Abrikosov suggests an elegant approach, however, and I would like to understand the details.

The problem requires no particular background in condensed matter physics, as the main result is boiled down to computing an integral, which I quote directly from the paper:

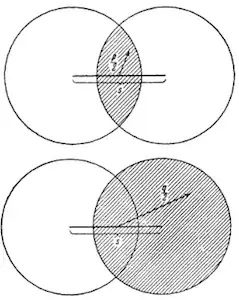
In terms of these variables, $E^{(2)}$ takes on the form $$E^{(2)} = -\dfrac{mU^2}{4\,(2\pi\hbar)^9}\int\!\mathrm{d}^3\vec{\bf s} \int\!\mathrm{d}^3\vec{\bf p} \int\!\mathrm{d}^3\vec{\bf q} \ \dfrac{1}{{\bf p}^2-{\bf q}^2}$$ where the region of integration for the vector $\vec{\bf s}$ is $\ 0 < |\vec{\bf s}| < 2p_o\ $ and the range of values for $\vec{\bf p}$ and $\vec{\bf q}$ is shown in the figure.

If we introduce the variables $x_{\bf q} = \cos{({\bf q},{\bf s})}\ $ and $x_{\bf p} = \cos{({\bf p},{\bf s})}\ $, $\ E^{(2)}$ becomes $$E^{(2)} = -\dfrac{8mU^2\pi^3}{(2\pi\hbar)^9} \int_0^{2p_o}\!\!\!s^2\mathrm{d}s \int_0^1\!\!\! \mathrm{d}x_{\bf p} \int_0^{z(x_{\bf p})}\!\!\!p^2\mathrm{d}p\int_{-1}^1\!\!\!\mathrm{d}x_{\bf q}\int_0^{z(x_{\bf q})}\!\!\!q^2\mathrm{d}q \ \dfrac{1}{p^2-q^2} \ , \ $$ where $z(x)$ satisfies the relation $$z^2+2 z s x+s^2=4p_o^2 \ . \ $$ From this, by means of a series of transformations and partial integrations over $\mathrm{d}x_{\bf p}\ $ and $\mathrm{d}x_{\bf q}\ $ we find $$E^{(2)}=\dfrac{2mU^2p_o^7}{\pi^6\hbar^9}\!\!\!\int_0^1\!\!\!\!\!\!s^2\mathrm{d}s \left[ \int_0^{1+s}\!\!\!\!\!\!\!\!p^2\mathrm{d}p \int_0^{1-s}\!\!\!\!\!\!\!\!q^2\mathrm{d}q + \dfrac{1}{4s^2} \int_{\sqrt{1-s^2}}^{1+s}\!p\mathrm{d}p(1-p^2-s^2) \int_{\sqrt{1-s^2}}^{1-s}\!q\mathrm{d}q(1-q^2-s^2) \right]\frac{1}{p^2-q^2}.$$

Integrating further by parts over ${\bf s}$ and then carrying out the remaining integration, we obtain $$E^{(2)} = (6/35) (3/\pi)^{2/3} (11-2\log{2}) a N^{1/3} E^{(1)} \ .$$

As stated above, I am stuck at the line marked in Bold.

My attempts at a solution have resulted in some muddled results. I am unsure how to make them concrete, but they do check out in mathematica. I will list some of the steps that I have made:

1. There is an implicit change of variables $\ s'\to s/2p_o\ $ and the same for $\ z,\ p,\ $ and $q$.
2. By means of partial integrations over $\mathrm{d}x_{\bf p}\ $ and $\mathrm{d}x_{\bf q}\ $ , $\ E^{(2)}$ becomes (apart from constants) $$\int_0^{1}\!\!\!\! s^2\mathrm{d}s \left( \int_{0}^{z_1}\!\!\!\!\!\! \mathrm{d}p \int_{0}^{z_{-1}}\!\!\!\!\!\!\!\! \mathrm{d}q \ \ + \int_{0}^{z_1}\!\!\!\!\!\! \mathrm{d}p \int_{z_0}^{z_{-1}}\!\!\!\!\!\!\!\! x(q)\,\mathrm{d}q \ - \int_{z_0}^{z_1}\!\!\!\!\!\! x(p)\,\mathrm{d}p\!\! \int_{0}^{z_{-1}}\!\!\!\!\!\!\! \mathrm{d}q \ - \int_{z_0}^{z_1}\!\!\!\!\!\! x(p)\,\mathrm{d}p\!\! \int_{z_0}^{z_{-1}}\!\!\!\!\!\!\!\! x(q)\,\mathrm{d}q \right) \dfrac{p^2 q^2}{p^2-q^2}$$ where $ \ x(z) = (2sz)^{-1} (1-z^2-s^2) \ $, and $\ z_x\ $ are roots of $\ z^2+2 z s x+s^2=1 \ $ for $\ x=1,\ 0,\ $ etc., namely, $ \ z_0 = \sqrt{1-s^2} \ $ , $ \ z_1 = 1-s \ $ , $ \ z_{-1} = 1+s \ .$
3. By means of a set of $u$-substitutions, e.g., $2s u=z_o^2 -p^2$ and similar substitutions, $\ E^{(2)}$ transforms to (apart from constants) $$\int_0^{1}\!\!\!\! s^2\mathrm{d}s \int_{0}^{z_1}\!\!\!\!\!\!\! p\,\mathrm{d}p \int_{0}^{z_{-1}}\!\!\!\!\!\!\! q\,\mathrm{d}q \left( \dfrac{p q}{p^2-q^2} + s\ \dfrac{p}{z_0^2-p^2+2sq} + s\ \dfrac{q}{z_0^2-q^2-2sp} +\dfrac{s}{2} \dfrac{1}{p+q} \right)$$
4. Recognize at this point that the middle two terms must equal $\ (-2)\ \times \ $ the final term, then the result in the paper is obtained if one can show that (?) $$\int_0^{1}\!\!\!\! s^3\mathrm{d}s \int_{0}^{z_1}\!\!\!\!\! p\,\mathrm{d}p \int_{0}^{z_{-1}}\!\!\!\!\!\!\! q\,\mathrm{d}q \left( \dfrac{1}{p+q} + \dfrac{p}{z_0^2-p^2+2sq} + \dfrac{q}{z_0^2-q^2-2sp} \right) \ =^{\bf ???} \ 0 \ .$$
5. To facilitate a contour integral to show that the integral vanishes, go back to the first step and extend the domain to infinity by a change of variables (familiar from relativistic mechanics) $$ p’ = \dfrac{p}{\sqrt{1 - s^2}} \ \ , \ \ q’ = \dfrac{q}{\sqrt{1 - s^2}} \ \ , \ \ s’ = \dfrac{s}{\sqrt{1 - s^2}} \ \ , \ \ z’ = \dfrac{z}{\sqrt{1 - s^2}} \ \ , $$ which results in a change in the root equations: $$(z’)^2+2 z’ s x-1=0 \ , \ $$ and $ \ z’_0 = 1 \ $ , $ \ z’_1 = \sqrt{1+s^2}-s \ $ , $ \ z’_{-1} = \sqrt{1+s^2}+s \ .$ The problem reduces to show that (?) $$\int_0^{\infty}\!\!\!\! \dfrac{s^3\mathrm{d}s}{(1 + s^2)^{9/2}} \int_{0}^{z’_1}\!\!\!\! p\,\mathrm{d}p \int_{0}^{z'_{-1}}\!\!\!\! q\,\mathrm{d}q \left( \dfrac{1}{p+q} + \dfrac{p}{1-p^2+2sq} + \dfrac{q}{1-q^2-2sp} \right) \ =^{\bf ???} \ 0 \ \ \ ({\bf ???})$$
6. Can I perform a contour integral over $s$ to show this is zero? How do I handle the $s$ appearing in the limits? Recalling that the goal was merely to eliminate the integrals with a single factor of "$\ x\ $" in step (2.), have I strayed too far from the path to get here?
7. Are there more transformations like this that I have missed?

BOTTOM LINE: How and which "transformations" were used to obtain the final square brackets integral expression in the paper, with just two very symmetric terms?

Answer 1

After your step 2, you you just need to use the symmetries of the integral like you already have, to drop additional terms that are zero. As you must have noticed since you changed the $x_q$ limits to be from $-1$ to $0$, the integrand of the original integral changes sign under the interchange of $p$ and $q$. Therefore, regions where the $p$ and $q$ integrals are the same give zero.

A related symmetry is that the integrand $f(s)$ of the final $s$ integral \begin{equation*} \begin{split} I &= \int_0^1 ds s^2 f(s) \\ f(s)&=-\int_0^1 dx_p \int_0^{z(x_p)}dp p^2 \int_0^{-1} dx_q \int_0^{z(x_q)} dq q^2 \frac{1}{p^2-q^2} \end{split} \end{equation*} is antisymmetric, that is $f(s)=-f(-s)$. You can see this since $z(x)=\sqrt{1-s^2(1-x^2)}-sx$, so that if $s\rightarrow -s$, $z(x)\rightarrow z(-x)$. The integrand therefore becomes \begin{equation} f(-s)=-\int_0^1 dx_p \int_0^{z(-x_p)} dp \int_0^{-1} dx_q \int_0^{z(-x_q)} dq \frac{p^2q^2}{p^2-q^2} \,. \end{equation} Now changing variables to $x_p'=-x_q$, $x_q'=-x_p$, $p'=q$, $q'=p$, this becomes \begin{equation} f(-s)=\int_0^{-1} dx_q' \int_0^{z(x_q')} dq' \int_0^{1} dx_p' \int_0^{z(x_p')} dp' \frac{p'^2q'^2}{p'^2-q'^2} \,, \end{equation} and noting that the primed dummy variables are now integrated over the same domain as the unprimed, $f(s)=-f(-s)$.

This means we can replace $f(s)$ with $[f(s)-f(-s)]/2$, or equivalently drop any terms in $f(s)$ that are symmetric in $s$.

Integrating $x_p$ and $x_q$ by parts gives the integrand to be \begin{equation} f(s) = -\left [ \int_0^{1-s}dp -\int_{\sqrt{1-s^2}}^{1-s} dp \frac{1-s^2-p^2}{2sp}\right] \left [ \int_0^{1+s}dq -\int_{\sqrt{1-s^2}}^{1+s} dq \frac{1-s^2-q^2}{2sq}\right] \frac{p^2q^2}{p^2-q^2} \end{equation} which is the $s$ integrand of your step 2. The first $p$ with the first $q$ integral, and the second $p$ with the second $q$ integral, are antisymmetric in $s$. The sum of the cross terms is symmetric in $s$. We therefore can drop them. The first integral becomes \begin{equation*} -\int_0^{1-s}dp \int_0^{1+s} dq \frac{p^2q^2}{p^2-q^2} = \int_0^{1+s}dp \int_0^{1-s} dq \frac{p^2q^2}{p^2-q^2} \end{equation*} where the equation uses the antisymmetry in either $s$ or $p \leftrightarrow q$ to write the integral in the form given in the paper. Similarly the other surviving integral becomes \begin{equation*} -\int_{\sqrt{1-s^2}}^{1-s} dp \frac{1-s^2-p^2}{2sp} \int_{\sqrt{1-s^2}}^{1+s} dq \frac{1-s^2-q^2}{2sq} = \int_{\sqrt{1-s^2}}^{1+s} dp \frac{1-s^2-p^2}{2sp} \int_{\sqrt{1-s^2}}^{1-s} dq \frac{1-s^2-q^2}{2sq} \end{equation*} which again is in the form of the paper. The result is \begin{equation*} I = \int_0^1 s^2 ds f(s) \end{equation*} with \begin{equation*} f(s)= \left [ \int_0^{1+s}dp \int_0^{1-s} dq + \int_{\sqrt{1-s^2}}^{1+s} dp \frac{1-s^2-p^2}{2sp} \int_{\sqrt{1-s^2}}^{1-s} dq \frac{1-s^2-q^2}{2sq} \right] \frac{p^2q^2}{p^2-q^2} \,. \end{equation*} The authors may have done something somewhat different now, but at this point, the $p$ and $q$ integrals can be done by expansion in partial fractions, with integrating by parts to simplify integrals of logarithms. Regions where $p$ and $q$ are integrated over the same values give zero, so in the first integral, we can drop the part where $0<p<1-s$. In this case, $p>q$ for both integrals. For $p>q$, \begin{equation} \begin{split} \int dp \int dq \frac{p^2q^2}{p^2-q^2} &= -\frac{(p^2-q^2)pq}{4}+\frac{p^4-q^4}{8}\ln\left (\frac{p+q}{p-q}\right) \\ \frac{1}{4s^2} \int dp \int dq (1-s^2-p^2)(1-s^2-q^2)\frac{pq}{p^2-q^2} &= \ln\left (p^2-q^2\right) \left [ (p^2-q^2)\left (\frac{1}{8}-\frac{1}{16s^2}-\frac{s^2}{16}\right ) \right . \\ & \left . +(p^4-q^4)\left (\frac{1}{16s^2}-\frac{1}{16}\right) -(p^6-q^6)\frac{1}{48s^2} \right ] \\ & -(p^2-q^2)\frac{p^2q^2}{48s^2} \end{split} \end{equation}

Plugging these in, the terms become \begin{equation} \begin{split} \int_0^{1+s}dp\int_0^{1-s} dq \frac{p^2q^2}{p^2-q^2} = \int_{1-s}^{1+s} dp \int_0^{1-s} dq \frac{p^2q^2}{p^2-q^2} &=s^3-s-(s^3+s)\ln(s) \\ \int_{\sqrt{1-s^2}}^{1+s} dp \frac{1-s^2-p^2}{2sp} \int_{\sqrt{1-s^2}}^{1-s} dq \frac{1-s^2-q^2}{2sq} \frac{p^2q^2}{p^2-q^2} &= \frac{s^2(s^2+3)}{6}\ln \left (\frac{1+s}{1-s}\right) +\frac{s(3s^2+1)}{6}\ln\left [ s^2(1-s^2)\right] \\ & -s\left (s^2+\frac{1}{3}\right) \ln(2s) - \frac{s(s^2-1)}{3} \end{split} \end{equation} The $s$ integrals are now straightforward. You can integrate by parts in $s$ to simplify the log integrals. The result is \begin{equation} \begin{split} I &= \int_0^1 ds s^2\left [ s^3-s-(s^3+s)\ln(s) +\frac{s^2(s^2+3)}{6}\ln \left (\frac{1+s}{1-s}\right) +\frac{s(3s^2+1)}{6}\ln\left [ s^2(1-s^2)\right] \right . \\ & \left . -s\left (s^2+\frac{1}{3}\right) \ln(2s) - \frac{s(s^2-1)}{3} \right] =\frac{1}{840} \left [11-2\ln 2\right] \end{split} \end{equation} and shows the $11-2\ln 2$ result.