3

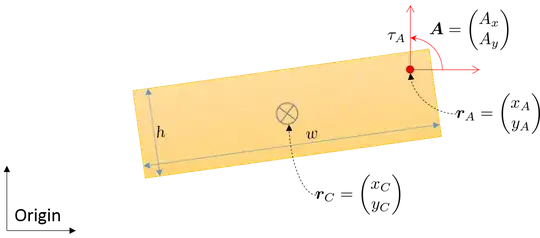
I would like to calculate the angular acceleration of an object on which a force $F$ is applied at point $P$. The scene is 2D, and the complex object consists of many axis-aligned rectangles.

I calculated the mass center $O$ with the weighted average of the centroids of the rectangles.

After that the direction vector $r$ is $P-O$, and the torque can be calculated as: $ \tau = r \times F $, which in the 2D case is: $ r_x F_y - F_x r_y $

The angular acceleration can be calculated as $ \alpha = \frac{\tau}{I} $ where $I$ is the moment of inertia.

This is where I'm stuck. I have to calculate the moment of inertia of this object. I've found a page with the moments of area of simple objects. It says, that for a rectangle:

$$ I_x = \frac{bh^3}{12} $$ $$ I_y = \frac{b^3h}{12} $$

Why does the inertia has an $x$ and $y$ component? Almost all of the rectangles of my object have a diferent centroid from the origin. Where will the position and mass properties of the rectangles be used when calculation the moment of inertia?

Update

I solved the problem using this list, and the parallel axis theorem. The moment of inertia is:

$$ I = \sum_{i \ \in \text{ rectangles}} \frac{m_i}{12}(h_i^2 + w_i^2) + m_i (O_x - C_{i_x})^2 + m_i (O_y - C_{i_y})^2 $$

Where $C$ contains the centroids, $w$ and $h$ the sizes, and $m$ the masses of the rectangles.

Iter Ator
  • 317

3 Answers3

1

The parallel axis theorem:
Given the moment of inertia $I_0$ of an object with mass $m$ about its center of mass, then the moment of inertia about a parallel axis that is displaced by a (perpendicular) distance $r$ is $I_0 + mr^2$.

You may also need to know the perpendicular axis theorem: for a thin lamina, the moment of inertia about an axis through the center of mass, perpendicular to the lamina, is equal to the sum of the moments of inertia about two perpendicular axes in the plane. So if your rectangle is centered on the origin in the XY plane, then the moment of inertia about the Z axis is found from $I_Z = I_X + I_Y$

This should allow you to figure out how to solve your problem.

sammy gerbil
  • 27,586
Floris
  • 119,981
0

The mass moment of inertia about the z (out of plane) of a 2D rectangle, as measured on the centroid, is $$I = \frac{m}{12} (w^2+h^2)$$ where $w$ is the width and $h$ the height.

So consider the general case of a 2D force with components $A_x$ and $A_y$ applied on a body, as well as a torque $\tau_A$ at a point A with coordinates $x_A$ and $y_A$.

EOM1

The equations of motion track the motion of the center of mass with coordinates $x_C$ and $y_C$ as well as the orientation angle $\theta$.

$$\begin{aligned} A_x & = m \ddot{x}_C \\ A_y & = m \ddot{y}_C \\ \tau_A-A_x (y_A-y_C) + A_y ( x_A-x_C) & = I \ddot{\theta} \end{aligned} $$

Now to answer the more general question, of how to calculate MMOI for 2D shapes.

  1. Assume solid has uniform thickness $t$ in the plane, and define a small volume element $${\rm d}V = t\, {\rm d}A$$
  2. The total mass is thus calculated from the volume using a uniform density $\rho$ $$ m = \int \rho\, {\rm d}V $$
  3. The center of mass is calculated with a similar integral $$ \pmatrix{x_C \\ y_C} = \frac{1}{m} \int \rho \pmatrix{x\\y} {\rm d}V $$
  4. Finally the mass moment of inertia about the center of mass is $$ I = \int \rho\, (x^2+y^2) {\rm d}V $$

You can use the above to calculate the MMOI of a rectangle spanning $x = -\frac{w}{2} \ldots \frac{w}{2}$ and $y = -\frac{h}{2} \ldots \frac{h}{2}$, with ${\rm d}A = {\rm d}x\, {\rm d}y$

  • Mass $$ m = \rho \int \limits_{-\frac{h}{2}}^{\frac{h}{2}} \int \limits_{-\frac{w}{2}}^{\frac{w}{2}} t\,{\rm d}x\, {\rm d}y = \rho\, t\, w\, h $$ $$ \rho = \frac{m}{t\,w\,h} $$
  • MMOI $$ I = \rho \int \limits_{-\frac{h}{2}}^{\frac{h}{2}} \int \limits_{-\frac{w}{2}}^{\frac{w}{2}} t\,(x^2+y^2) {\rm d}x\, {\rm d}y = \rho \frac{t\,w\,h (w^2+h^2)}{12} $$ $$ I = \frac{m}{12} ( w^2+h^2 )$$
John Alexiou
  • 40,139
-1

You need to calculate the center of mass of the components by using sum (m1 times dx 1to m_n times dxn)/ (m1+.....+ M_n).

Then your angular inertia is I= sum (m* dx^2 + m*dy^2) + Sum of each part's angular moment of inertia individualy. By dx and dy we mean the distance between the CG of each component to the CG of the integrated final shape.

Your torque is Fp

P is your torque arm, but has to be adjusted to bew CG of the system , and F the force.

And your angular acceleration, omega = I* torque.

kamran
  • 1,655