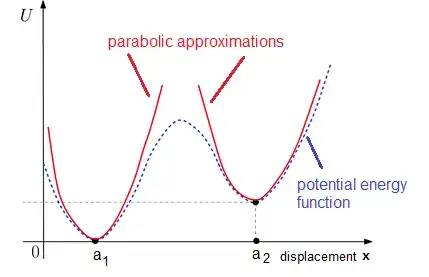
So in my classical mechanics book it states:
"For any sufficiently small displacement, any system of this kind behaves like a harmonic oscillator."
When discussing SHO. So I am curious what is considered to be "sufficiently small". Like with a spring I can extend it to a certain length and it will be so far from the equilibrium that deformation occurs and obviously at that point the spring will no longer behave as an oscillator, is this a good interpretation? I feel like it's not what is meant. I understand that Hooks law is derived from the maclourine series of potential energy and that because of that it has to be sufficiently close to equilibrium but what is considered "close"?