How can a pendulum have amplitude greater than $\pi$?

Question

How can a pendulum have amplitude angle greater than $\pi$? I've been reading about phase plots, which are graphs of the $\frac{d\theta}{dt}$ on the $y$ axis and $\theta$ on the $x$ axis, shown below.

I can understand that the curves are not perfect ovals because we cannot use the small angle approximation. I can also see that there is one curve in the right side's drawing which looks like a sine curve shape, but intersects the $x$ axis at $\pi$ and $-\pi$.

But how are the other curves i.e. the curve intersecting $y$ axis at +2 created? What equation gives that and how would the pendulum's motion look? How would such an equation be derived?

I have a pendulum equation $$\frac{d\theta}{dt}=\pm\sqrt{\frac{2g}{l}(1-cos\theta_A)}$$ ($\theta_A$ is amplitude)

I derived that with conservation of energy laws, like for a simple pendulum but I did not do the small angle approximation. I tried to put $\theta_A=\pi+1$ and I got a simple oval, not the pair of curves that is symmetric about the $x$ axis. I do not understand the math and notation being used in this question: What is the period of a physical pendulum without using small-angle approximation?

I'm confused.

Answer 1

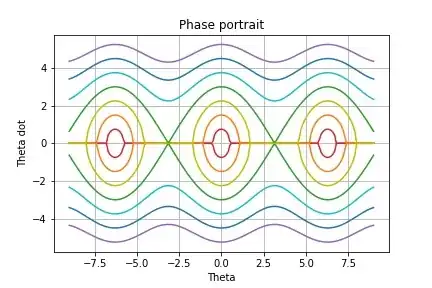
How are the other curves i.e. the curve intersecting y axis at +2 created?

The trick behind understanding that phase portrait is realizing that the 'amplitude' is not the fundamental quantity which acts as the difference between those lines.

The amplitude of a pendulum is usually considered to be the angle or displacement at which the velocity is zero, according to conventional intuition. But we see that the line you pointed out, the one with a maximum angular velocity of $2$, never reaches $\frac{d\theta}{dt}=0$, so a 'pendulum'described by that line won't have an amplitude according to our usual definition.

The solution? You need to think of maximum angular velocity as the fundamental quantity instead. For every pendulum shown by that phase portrait, the maximum angular velocity will be at the lowest point of the pendulum's trajectory. So each line in that phase portrait depicts a different trial with the same pendulum, except the angular velocity at that lowest point is different each time.

Think of performing an experiment to test the behavior of your pendulum for different amplitude angles, but each trial, instead of dropping the pendulum from a different position, you launch it from that same base point with a different velocity. And obviously $v=l\dot{\theta}$, where $\frac{d\theta}{dt}=\dot{\theta}$, so you'll be starting with different initial angular velocities.

What equation gives that and how would the pendulum's motion look?

Now let's consider you start the pendulum with a really high angular velocity... it'll eventually end up moving in a complete circle! When the pendulum reaches $\theta=\pi$, it'll still have some kinetic energy, and it'll descend on the opposite 'side' of the pendulum's pivot.

When you're at the lowest point, you'll have the greatest velocity and hence the greatest angular velocity. As the height increases, the potential energy increases, hence the kinetic energy decreases and the angular velocity decreases. And thus you see a minimum, but nonzero angular velocity when $\theta=\pi$ according to the phase portrait.

How would such an equation be derived?

Conservation of energy works again, though the Lagrangian may be easier. You know the initial kinetic energy, because your initial conditions give you $l$ and $\dot{\theta}_{max}$. Also, at any angle $\theta$, the potential energy is $mgl(1-\cos\theta)$. If you consider the energy at a couple of different points and equate them, you'll get $$\dot{\theta}=\pm\sqrt{\dot{\theta}_{max}^2-\frac{2g(1-\cos\theta)}{l}}$$

I may have mentioned that I'm a huge fan of ultra-colorful diagrams, so here's one I threw together. It's much clearer than the monochrome thing in the question.

Answer 2

Have you ever played on a playground swing, and got worried that if you went any faster, you would swing right over the bar and start going around and around? That's what's happening here. If you give the pendulum more energy than $2 m g \ell$, then it'll get to the top and keep going, swinging around and around. Strictly speaking it has no amplitude, since it isn't oscillating.

Answer 3

On your phase portraits, the horizontal axis is $\theta$, and the vertical axis is proportional to $\dot \theta$. Each trajectory (red line) corresponds to a constant energy. The trajectory that intersects the horizonal axis is one that has enough energy to just make it's around a full circle about the pivot. The trajectories like the one you specify that go to +2 on the vertical axis are trajectories that have much more energy, where the pendulum is spinning "rapidly" around the pivot point. In this case there is no amplitude in $\theta$. You also have to keep in mind that time is not explicit on these phase portraits.

For a simple pendulum, another way to write the equation of motion is $\ddot \theta =\frac{g}{L} sin(\theta)$. This equation does not have a solution $\theta (t)$ we can write out with simple functions in general. It must be solved numerically. If we use the small angle approximation, then we can get a nice solution written in terms of sines and cosines. Of course, if we are looking at the phase portrait, then the equation of $\dot \theta (\theta)$ is a perfectly valid way to see "how the pendulum's motion would look", as you asked in your question. The phase portrait does not tell us the rate at which we travel along a trajectory in the phase space, but this is not needed to understand much of this system qualitatively.

I have already mentioned an answer to the title question, but I will address it more explicitly here. The pendulum cannot have an amplitude larger than $\pi$. Amplitude is defined by the largest $\theta$ can be. You can see the the higher energy trajectories do not have a maximum $\theta$, as $\theta$ either increases or decreases forever. Even if you restrict your range of $\theta$ to just be in the range of $[-\pi ,\pi ]$ in these large energy cases, your "amplitude" is now $\pi$ and cannot be any larger.