Explicit equation for scale factor - how long valid?

Question

In “The picture of our universe: A view from modern cosmology” (https://arxiv.org/abs/astro-ph/0209504 - eqn 63, page 26) there's an explicit equation for the scale factor for a flat universe with $\Omega_{M}+\Omega_{\Lambda}=1=\Omega_{\text{total}}$:$$a\left(t\right)=A^{1/3}\sinh^{2/3}\left(\frac{t}{t_{\varLambda}}\right),$$where $A=\Omega_{m,0}/\Omega_{\varLambda,0}$ and $t_{\varLambda}=\frac{2}{\sqrt{3\varLambda}}$. For how long in the history of the universe has the $\Omega_{M}+\Omega_{\Lambda}=1=\Omega_{\text{total}}$ condition been true and how is this known?

Answer 1

I'll make some rough estimates, doing everything to the nearest order of magnitude. That will be good enough, because it's not like your equation will suddenly stop working at some certain time, it'll just gradually degrade as we go back in time.

We know that the radiation contribution today is $$\Omega_{r,0} \approx 10^{-4}.$$ We also know the matter density falls off as $1/a^3$, while the radiation density falls off as $1/a^4$, so $$\frac{\Omega_m}{\Omega_r} \propto a$$ which indicates matter and radiation were equally important at around $a_{\text{eq}} \sim 10^{-4}$. For smaller scale factors, your result surely doesn't hold.

If you want to convert this into a time since the Big Bang, you can use the heuristic that the Hubble parameter $H = \dot{a}/a$ should obey $$H \sim \frac{1}{t}$$ where $t$ is the current age of the universe. This is true whenever the universe is dominated by a single component which isn't dark energy, essentially by dimensional analysis. The Friedmann equation may be rewritten as $$H(a)^2 = H_0^2 (\Omega_{r,0} a^{-4} + \Omega_{m,0} a^{-3} + \Omega_{k,0} a^{-2} + \Omega_{\Lambda, 0})$$ where $\Omega_{k,0}$ is a term that formally accounts for the curvature of the universe. We know that at the current moment, $$\Omega_{k,0} \approx 0, \quad \Omega_{r,0} \approx 0, \quad \Omega_{m,0} + \Omega_{\Lambda,0} \approx 1.$$ Also note that since the curvature term falls off as $a^{-2}$, it becomes less and less relatively important in the early universe compared to matter and radiation, so we never have to worry about it. (In particular, if the density is almost critical now, it was even closer to critical in the past.) Counting only the radiation at time $a_{\text{eq}}$ for simplicity, $$H(a_{\text{eq}})^2 = H_0^2 \frac{\Omega_{r,0}}{a_{\text{eq}}^4} \approx H_0^2 a_{\text{eq}}^{-3}, \quad H(a_{\text{eq}}) \approx 10^6 H_0.$$ Therefore, the age of the universe at time $t_{\text{eq}}$ is $$t_{\text{eq}} \approx 10^{-6} t_0 \sim 10^4 \text{ years}.$$ Your equation should begin to be fairly accurate after about $10^5$ years.

Answer 2

The exact relationship between the scale factor “a” and cosmic time “t” for our universe, considered flat, is given by the following expression:

$$\displaystyle t=\dfrac 1{H_0} \int_0^{a} \dfrac{dx}{\sqrt{\Omega_{\Lambda_0} x^2+\Omega_{M_0} x^{-1}+\Omega_{R_0} x^{-2}}}$$

The best values currently available (given for Planck Mission 2018), for the parameters are:

$H_0=67.66 \ (km/s)/Mpc$

$\Omega_{R_0}=9.15 \cdot 10^{-5}$

$\Omega_{M_0}=0.31105425$

$\Omega_{\Lambda_0}=0.68885425$

An approximation of the relationship between the scale factor and time for our universe, (considered flat), when the radiation density ratio is negligible, is given by the following expression:

$$\displaystyle a \approx \left (\frac{\Omega_{M_0}}{\Omega_{\Lambda_0}}\right )^{1/3} \sinh^{2/3}\left ( \frac{3 H_0 \sqrt{\Omega_{\Lambda_0}}}{2} \ t \right )$$

This expression is the same as in equation 63 page 26 of the document "The picture of our universe: A view from modern cosmology", taking into account that:

$\displaystyle t_{\Lambda}=\left (\dfrac 4{3\Lambda c^2} \right )^{1/2}=\dfrac{2}{3 H_0 \sqrt{\Omega_{\Lambda_0}}}$

For the density ratios in the approximate expression, we will use:

$\Omega_{M_0} \approx 0.3111$

$\Omega_{\Lambda_0} \approx 0.6889$

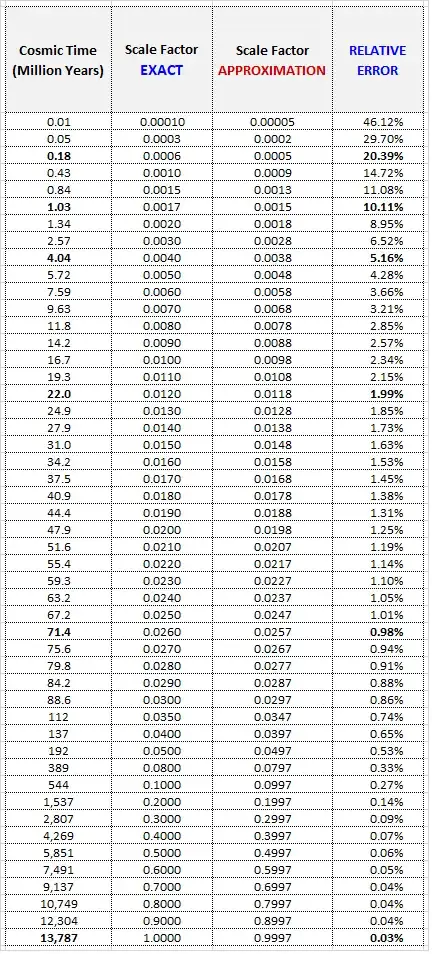
Now, we make a table in which for each cosmic time from the beginning until now, we tabulate the scale factor calculated with the exact expression (by numerical methods), the scale factor calculated with the approximate expression, and the relative error we make if we keep the approximate expression.

The value of the error we accept will determine from what cosmic time the approximate expression is acceptable

• If we do not accept an error greater than 20% the approximation is valid from t=180 thousand years until now.

• If we do not accept an error greater than 10% the approximation is valid from t=1 million years until now.

• If we do not accept an error greater than 2% the approximation is valid from t=22 million years until now.

• And if we only accept an error of less than 1% the approximation is valid from t=71 million years until now, ...

Best regards.

Answer 3

Yes, $\Omega_{M}+\Omega_{\Lambda}=1=\Omega_{\text{total}}$ implies that the universe is flat. A spatially flat universe requires $K = 0$, with $K$ the curvature constant. As you may be aware of this constant can also have the values $-1$ or $+1$ in case the spatial curvature is hyperbolic or spherical respectively.

Now for a given universe $K$ can't change. A change from e.g. flat to spherical can't happen and moreover would imply a change of the topology. What changes in the flat case is the ratio $\Omega_{\Lambda}/\Omega_{M}$. It increases, but the sum of the dimensionless densities remains $constant = 1$.