Is flying really easier on smaller scales?

Question

In the book Playing with Planets, the author makes the following argument, pertinent to flying robots of the future:

As it is, an important law of physics says that smaller organisms fly much more easily than larger ones. This can be seen clearly in living organisms: small animals have a lot less trouble getting off the ground than larger ones. Therefore, once miniaturization sets in, we can expect to see lots of small flying robots.

I'm familiar with the upper-limit for size of birds, but I don't know if it can be expressed as a simple law of physics versus complications with the feather replacement intervals. On the other hand, insects have some of the highest mass-specific metabolisms of any animals on Earth. Most people's experience with RC helicopters is probably consistent with this - the flight time is typically a matter of minutes, severely limiting its usability. Large aircraft can fly clear across the world!

For all of these reasons, the idea scaling laws would be favorable to small flying robotic drones seem to violate intuition. Is there any truth to the idea that smaller flying machines would fly easier?

Is there an argument that can be made with Reynolds numbers? Tiny gnats can have Reynolds numbers in the 100s. Would laminar conditions set a lower limit on flight? How does scale affect the specific energy consumption needs of flying machines?

Answer 1

There's an interesting book by H. Tennekes on the subject of scaling in flying. If you want to go fast and far then the size of your plane scales up, while the speed of sound gives a limit, approached by a Boeing 747. But if you simply want to get off the ground with little effort (what was meant by "easy" in my book), then it is worth while to be small (I expect the force of a muscle to go like $\text{diameter} ^2$,  and not $\sqrt {\text {diameter}}$    (as claimed by @miceterminator, apologies to @AlanSE whom I confused him with).

According to Tennekes, the lift of a wing scales as $l^2.v^3$, where $v$=velocity and $l$ is length of wing. The weight scales like $\text{size}^3$, but for small things $l$ can be much bigger than size (in all directions) . For small things, $v$ can therefore be kept small. So, if you are small it is easier to get off the ground, but you go slower, and indeed the wind will become a greater adversary, and, so far, nothing is said about how long you can stay off the ground.

Note now, that solar energy will scale as $\text{size}^2$. Drag scales as $\text{size}^2.v^3$, and the energy needed per unit of time is drag$.v$, so we find that the "difficulty of flying" on solar energy, at all scales, scales as $v^4$, where size cancels out. Now you see that being small helps. What matters now is that our information processing must be squeezed into tiny devices. This should be possible if we just wait for Moore's law to do its job.

Answer 2

Seems to me your question contains two physics questions which depend on the definition of "easier". Certainly in an atmosphere it is easier to balance gravity the larger the ratio of surface to weight due to the viscosity of the medium.

On the other hand this does not make "easier" the maneuverability of the system in energy demands. So you are asking about the efficiency of energy consumption using small robots.

I would say that a small bee like robot would consume proportionally more energy according to its size and the viscosity of the medium. If it is fed energy wirelessly though the advantage of size for exploration is evident. Larger robots would need to carry their energy producing sources.

It is an engineering problem where all these questions should be balanced. There is probably a range of optimum size for each situation and demand in energy.

Answer 3

Leaving alone the feathers and everything, I would look at the power law. As I am unaware of the powerlaw concerning fluids (e.g. the interaction with air in this case), I would even ignore it and look at the drivetrain. As most birds take off more like choppers and less like planes (landing on spot) they need most of their muscle for liftof and can glide later on.

1. Now we assume that the force of a muscle goes with the $\text{diameter}_{muscle}^2 \propto F$ and
2. lets assume the lift of a wing is proportional to its area.
3. If the force that is neccessary to "drive" the wing is proportional to the area then ${\text{diameter}_{muscle}}^2 \propto A_{Wing}$
4. Now the volume and therefor the weight of the muscle goes with $\text{diameter}_{muscle}^3$ there for the weight goes up faster than lift, if you scale up the bird. ($\frac{\text{Lift}}{\text{Weight}}=\frac{1}{\text{diameter}_{muscle}}$)

This corresponds to the observation that large birds need to run in order to take of.

Now back to the robots. I am unaware of any power laws concerning microrobots (size of the battery vs capacity and power, power of the engine vs size, lifting of the rotor vs size) but here I think it is crucial to look at the processing power. As birds rely on a simple, probably partly inherited neural net, they often fail in nontrivial environments (bird vs window, bird vs car, bird vs finding the open window). The demand on robots is much higher and therefor they need a much more sophisticated computing device. And I believe this to be the crucial point because the processing demand does not go down a lot if the size of your robot goes down, and you can not power a 30W TDP processor on an machine thats the size of your thumb. You could probably design stupid robots that act as a swarm, (as birds do) but then the "size" is big as well even if discretized. As most of the development is probably funded by the military and you aim for military applications, loading off the processing to an external computer is not an option because the signal could easily be interrupted. Oh and if the original idea behind the quote is to go into scales where your robots can be lift by airflow itself, it wouldn't be much use as you probably could not steer it in an arbitrary direction of you would have a very short range.

Answer 4

Regarding large airplanes, a 747 can go more than halfway around the globe if it is flown high enough, and slow enough to maximize L/D (ignoring wind).

According to Wikipedia, jet aircraft range $R$ follows this law:

$$R=\frac{2}{c_T} \sqrt{\frac{2}{S \rho} \frac{C_L}{C_D^2}} \left(\sqrt{W_1}-\sqrt{W_2} \right)$$

$c_T$ is fuel flow rate per unit of thrust, and $W_1$, $W_2$ are initial and final weight. You can find the rest of the definitions on that link.

It says if you scale up the weight by four, you double the range.

For propeller-driven aircraft, it's a different story:

$$R=\frac{\eta_j}{c_p} \frac{C_L}{C_D} ln \frac{W_1}{W_2}$$

Where $c_p$ is fuel flow rate per unit of power.

It says range is not affected by weight, rather it is logarithmic in the ratio of initial to final weight. (Seems surprising.)

Answer 5

The lift to drag coefficient is $C_l/C_d$. The metric is important, as it basically dictates the energy consumption per unit distance traveled per unit mass, regardless of how fast the thing is traveling or how big it is.

I found some interesting references that show that this lift to drag ratio drops like a rock for small Reynolds numbers.

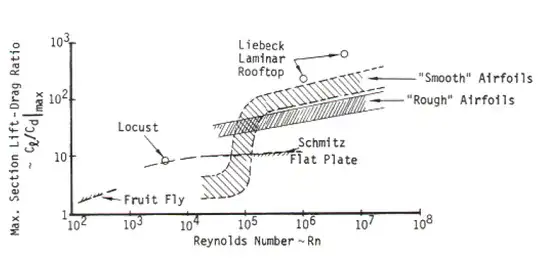
As I looked at that region around the gnat, I thought looked mostly proportional to Reynolds number. Reynolds number in this case is $ v L \rho / \mu $ where $L$ is a general proxy for the linear scale of the thing. But there's a larger problem here - that we're looking at drag coefficients for low Reynolds number. That doesn't make sense, since we're in the region of Stokes' Drag, not turbulent drag. After thinking about it, the low Reynolds number of the above graph made sense if you assume:

• Viscous forces increase the drag force
• The $1/2 \rho v^2 A$ proportionality still holds for lift

In other words, you can find the above proportionality to Reynolds number if you use the turbulent drag equation for lift and the laminar drag equation for drag. You can do this by just dividing them out, or you could create an "artificial" expression for $C_D$ using the below equation. It's artificial because it's supposed to be a shape factor, but we're out of the region of applicability for that.

$$ F_L = \frac{1}{2} \rho v^2 C_l A$$

$$ F_D = 6 \pi \mu L v $$

This makes sense to me, because there's no obvious improvement to be expected for lift from increased viscosity (note: this is almost the exact opposite claim of anna v's answer). A gnat makes a great energetic sacrifice in order to gain access to the ecological niche it inhabits. There are two other equations I want satisfied. One is that the lift is equal to the weight of the body and that the craft has enough energy to travel its full range ($x$). These follow in order of lift and energy.

$$ m g = \rho_b L^3 g = F_l$$

$$ F_d x = \nu L^3 $$

Here, $\nu$ is taken to be the energy density of the batteries or whatever the craft is using. From the equations I wrote I obtained these expressions:

$$ v = \sqrt{ L \frac{2 \rho_b g }{\rho C_L } } $$

$$ x = \frac{ \nu L^{3/2} }{12 \pi \mu} \sqrt{ \frac{2 \rho C_L }{\rho_b g} }$$

There are a few other metrics we're interested in. One is the power consumption, $v F_d$. That scales according to $L^{3/2}$. If you had some motor with a max power output that scaled as $L^3$, then scaling down would become difficult as you would need a larger motor relative to the size of the craft. This is consistent with the observation that flying insects have the greatest per-mass power consumption of most animals.

So far my answer has been awfully contrarian, since I share almost none of the conclusions of others. But let's look at one final metric, $1/2 m v^2$ compared to the total energy content. The kinetic energy relative to total energy ratio scales as $1/L^2$. That means that the needs of a runway are basically irrelevant on smaller scales. Because of that, it would definitely be easier for it to get up into the air.