Supersonic wind tunnel with total pressure loss?

Question

I am reading "I am reading "Fundamentals of Aerodynamics" 5th edition, J.D.Anderson. If you have the book, go to chapter 10: Compressible Flow through Nozzles, Diffusers, and Wind Tunnels".

In order to produce Mach 2.5 uniform flow in a laboratory, we can build a wind tunnel like this: 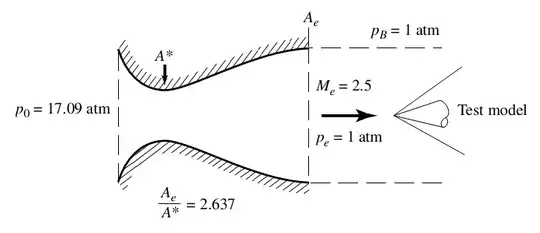The back pressure equals atmospheric pressure, the Mach 2.5 flow passes into the surroundings as a free jet. But we need high-pressure air supply at 17.09 atm which can be expensive, so we build this wind tunnel instead: 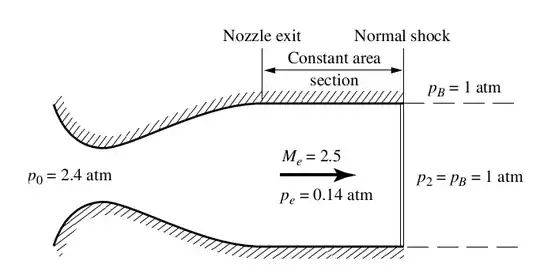A normal shock-wave stand right at the end of the wind tunnel. The reservoir with a pressure of only 2.4 atm which reducing the cost compared with the first wind tunnel.

Then the author said: A normal shock is the strongest possible shock, hence creating the largest total pressure loss. If we could replace the normal shock with a weaker shock, the total pressure loss would be less, and the required reservoir pressure $p_0$ would be less than 2.4 atm. So again, we build this instead: 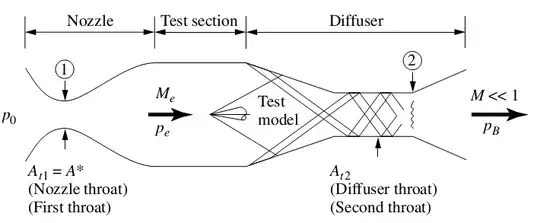with reflected oblique shocks behind the test section.

The objective is to have $p_o$ as low as possible and the exit pressure must be equal to atmosperic pressure (= 1 atm). But why is the $p_o$ in case 3 is smaller than $p_o$ in normal shock case ? You might think due to total pressure loss is smaller, but the final total pressures are not the same in two case, so how could we compare the $p_o$.

Answer 1

If we want the outflow pressure to be 1 atm, then we know the final pressure. We know for an oblique shock that the change in pressure across the shock is given by: $$ \frac{P_{2}}{P_{1}} = 1 + \frac{ 2 \ \gamma }{ \gamma + 1 } \left( M_{1}^{2} \ \sin^{2} \beta - 1 \right) \tag{1} $$ where the subscripts $1$ and $2$ correspond to the upstream and downstream regions, respectively, $\beta$ is the angle of the shock plane from the incident flow direction, $\gamma$ is the ratio of specific heats, $M_{j}$ is the Mach number in the $j$^th region, and $P_{j}$ is the average pressure in the $j$^th region. In the limit as $\beta \rightarrow 90^{\circ}$, i.e., a normal shock, we approach the following: $$ \frac{P_{2}}{P_{1}} = 1 + \frac{ 2 \ \gamma }{ \gamma + 1 } \left( M_{1}^{2} - 1 \right) \tag{2} $$ which is the standard pressure ratio change.

But why is the p_o in case 3 is smaller than p_o in normal shock case?

If you look at Equation 1 above, you will see that as $\beta \rightarrow 0$, the pressure ratio of the downstream to upstream drops considerably. That is, the maximum of Equation 1 is given by Equation 2, i.e., the case where the shock plane is orthogonal (or normal) to the incident flow.

This is why the 2nd P_o can be smaller than in the first case. The final/third example relates to Equation 1. You can generate the same M_e with a smaller pressure change by forcing the shocks to be oblique or you can reduce M_e to reduce the pressure change.

The 2nd nozzel/throat is a converging channel, which will kill the reflecting shocks. This is because shock waves are unstable in a converging channel, as I discussed at https://physics.stackexchange.com/a/137842/59023. This will further reduce the necessary pressure change, i.e., the combination of oblique shocks and a converging channel.