How does the electric field produced by a simple circuit look?

Question

I have not seen anywhere a description of how the electric field looks inside and around a simple circuit. For example let's say we have the circuit shown below. One DC voltage source, two resistors, and a constant current flowing around.

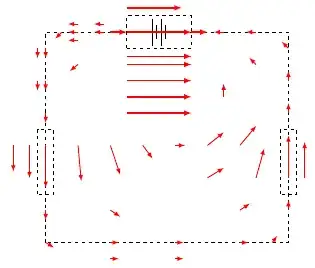
We know that the electric field inside the battery will point from positive to negative, we also know that the field inside the wires is very small and in the direction of the current. Through the resistors there will be a strong field pointing from positive to negative. But in order to maintain the relationship that a closed loop integral of the E field is zero everywhere we must also have a field outside of those circuit elements. I have no idea how this field will look but I have made a crude attempt at sketching it below.

Is this a realistic picture of how the field will look?

Answer 1

Close but not quite. Here's a very similar circuit from CircuitSurveyor. (I tried to input yours but it wouldn't calculate.) The background grid & flowlines are the Poynting vector $\mathbf S$. For the haphazardly scattered points, blue is $\mathbf E$, green is $\mathbf B$ (always into the screen here), and orange is $\mathbf S$. Note the $\mathbf E$ field near the wires is perpendicular to them, and wraps around circuit components.

Note this visualizer approximates the circuit as a 2D slice of an infinite circuit stack extending through the screen. A real instance would have non-zero $\mathbf B$ (and hence $\mathbf S$) outside the loop.

Answer 2

An electrical circuit is a lumped element model, that does not carry any geometrical information with it. Given a circuit you do not know what is the shape of the resistors, the dimension of the battery, the cross section of the wires, the position of the elements with respect to each other, and so on and so forth. Unless, you know those information by other ways, there is no way to even sketch the electric field.

Moreover, the idealized wires that connects the various components of the circuit are mere topological connections, they do not have any electric field inside.

a closed loop integral of the E field is zero everywhere

That is not what the second Kirchhoff's law says. It can easily be derived from the Faraday's law under the assumption that the magnetic field does not change.

$$\oint_{c} E \cdot \text{d}l=-\int_S \frac{\partial B}{\partial t}\cdot \text{d}S$$

Since, $B$ does not change with time its derivative is zero , thus

$$\oint_{c} E \cdot \text{d}l=0 \;\;\;\;\;\;\;\;\;\;\;\; \forall c$$

it must be true for all possible close loops c. This equation does not state anything about the field out of loop. Simply, it says that the sum of the electric field all around a loop is zero.

Answer 3

this video explains it somewhat clearly ;

https://youtu.be/bHIhgxav9LY?si=XU-59CKYqt31gt9M