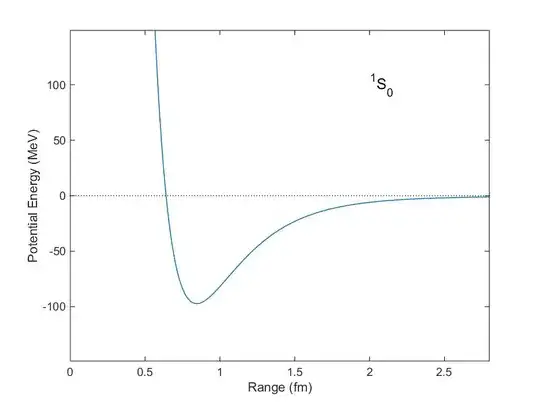
The potential energy associated to the interaction between nucleons has its minimum (point of equilibrium) at $r\sim 0.7 fm$, as showed in the following graph:
Nevertheless, there are two facts that are, apparently, in contrast with this:
- The average distance between nucleons is $\sim 1-2 fm$
- The average nucleon density is $\sim 0.17\,\,\ \mathrm{nucleons /fm^3}$
(These two are related because from the second follows a volume of $\sim 6 fm^2$ per nucleon which is in agreement with the average distance between nucleons)
So why is the average distance between nucleons usually greater that the $0.7 fm$ where the potential energy is minimum?
I'm aware that the "dimension" of nucleon is $\sim 1 fm$. But is this the reason why the distance between two of them cannot be much less?