$\bullet$ What are these (length) scales that we often talk about? Do we mean the wavelength of some Fourier modes of something?
Yes, these are the comoving wavelengths of Fourier modes (see next)
$\bullet$ If yes, do we mean the Fourier modes of the density fluctuations $\delta\rho/\rho$ or that of the inflaton field fluctuation $\delta\phi(\textbf{x},t)$ itself?
These are essentially one in the same: fluctuations of the inflaton field gives rise to curvature perturbations which manifest as density perturbations after inflation ends.
$\bullet$ Why should these scales leave or re-enter the horizon?
Comoving length scales grow along with the scale factor of the universe, which, during inflation, grows exponentially in time: $a(t) \sim e^{Ht}$. Meanwhile, the horizon, which is proportional to $H^{-1}$, is nearly constant during inflation. The quantity $aH = \dot{a}$ measures the ratio of a given comoving length scale to the horizon: how this quantity varies in time will tell us whether comoving length scales grow at a greater or lesser rate than the horizon. During inflation, $\dot{aH} = \ddot{a} > 0$, hence, scales eventually grow to lengths larger than the Hubble scale. Conversely, after inflation, $\ddot{a} < 0$ and they will eventually re-enter the horizon.
Here's a picture of how this happens during inflation:
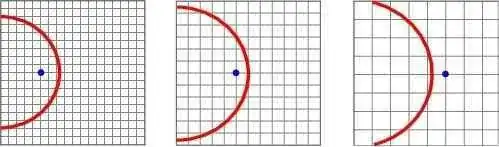
The red circle marks the horizon, which grows more slowly than the background during inflation. An object at rest with respect to the background (comoving) eventually overtakes the horizon.
$\bullet$ What is (are) the observable effect(s) of these scales?
These redshifted fluctuations give rise the well-known temperature anisotropies observed in the CMB. They eventually grow to form the large scale structure we see around us in the universe: galaxies, galaxy clusters, and so on.
$\bullet$ How do we distinguish between the roles of those length scales which first left and re-entered the horizon with those which always remained inside the horizon
It's really just a matter of scale. Perhaps this graphic will help:
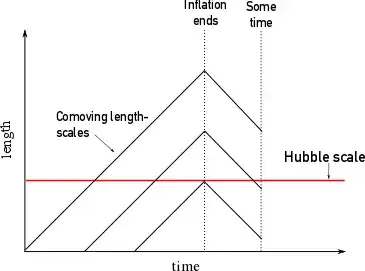
Here we have a couple different comoving length scales evolving during inflation (left of vertical "Inflation Ends" line) and after. Notice that those length scales that grow the largest by the end of inflation "started" first (this picture has meaning when we associate these length scales with the Fourier wavelengths of the scalar field fluctuations). There will of course by many scales that never grow to super-horizon sizes during inflation, having started too late.
Now, there is an important difference between the 'always subhorizon' and 'once superhorizon' modes in terms of the matter perturbations that they source. Superhorizon modes undergo a 'classical-to-quantum' transition, where they are manifested as curvature perturbations. As they re-enter the horizon, they source acoustic oscillations in the post-inflationary plasma; those that enter earliest oscillate for longer and so damp the most by the time the CMB is generated at recombination. So, the longest-wavelength modes are most evident in the temperature spectrum of the CMB (these are the large, broad peaks in the correlation spectrum).
Modes that never leave the horizon are in some sense "not real" because they never undergo the classical-to-quantum transition. They don't ever become bonafide curavture perturbations. Phenomenologically, this theoretical distinction is irrelevant, though, since any perturbations generated by such small wavelength modes would be damped out by recombination.

