Maximum acceleration to prevent rotation of body when held by a gripper

Question

MAIN QUESTION
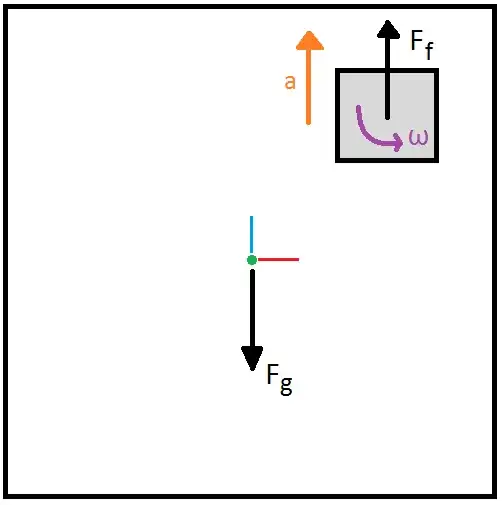
A mass body is held in place by a friction force. The object that generates this friction accelerates upwards. Because the acceleration is not acting inline with the center of mass of the body, the body starts to rotate around its contact point. Which is a result of the moment of friction that is not big enough to keep the body in place.

The main question is how to calculate the maximum linear acceleration to prevent any angular displacement of the body? (The acceleration is applied on the object that holds the body through the friction)

Some sub-questions that would help me are:

• How to calculate the moment of friction?
• How to translate the linear acceleration to a moment or angular momentum when it accelerates from the center of the friction connection?
• Is it correct to use the center of the friction connection as the "origin" of the calculation? (Moments, inertia and angular acceleration would be calculated relative to this "origin")

---

Previous formulation of the question. It gives more background information and an example situation of the question to clarify the question.

Context
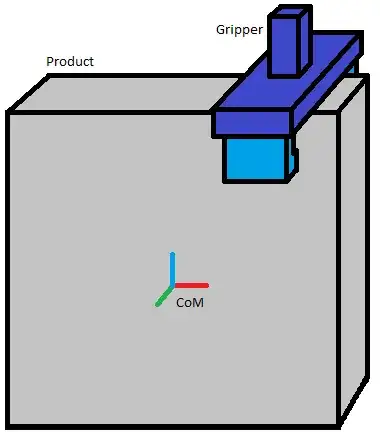
I am currently writing software that automatically calculates the maximum linear acceleration of a 6-axis robot when holding a product. The robot uses a gripper to pick and place products. The product may not displace or rotate relative to the gripper.

Problem
In the first place I assumed it would be as simple as: $\sum F=m*a$. But this would only suffice if the product is picked in its center of mass. When the product is not picked in its center of mass, the product starts to rotate a bit when the robot (de-)accelerates (Example situation can be seen in figure 1).

Thoughts so far...
Assumed is that the clamping force is evenly spread over the contact area between the product and gripper. The gravitational force generates a moment relative to the center of the contact area. The friction force is spread over the area which would generate a opposing moment. The acceleration of the gripper would generate an angular momentum.

These moments together with the differential of the momentum would then be implemented in: $$\sum M + \dfrac{\Delta L}{\Delta t} = I * \alpha$$ Then assume $\alpha = 0 \hspace{2mm}rad/s^2$ and calculate the maximal momentum. Which would need to be translated back to a linear acceleration ...

No idea if I am heading in the right direction. I cannot find any examples where a clamped body rotates around the center of the friction contact area due to linear motion.

Any help would be appreciated. Thanks in advance.

Answer 1

Your intuition is correct. The problem is as "simple" as applying Newton's 2nd Law for linear and rotational motions : $$\vec{F}-m\vec{g}=m\vec{a}$$ $$M-mgx=I\alpha$$ where $F$ is the resultant static friction force, $M$ is the moment of the friction forces, and $x$ is the horizontal distance of the centre of the friction force from the centre of mass of the block.

$\vec{F}$ can be deduced quite easily from the 1st equation. If there were no torques involved we could then assume that $F$ is spread uniformly over the gripping surface, and is everywhere in the same direction. Then we could apply $F\le \mu N$ to calculate the maximum acceleration for a given gripping force $N$.

Likewise if the applied forces amount to a pure torque, and we know the centre of rotation so that we can find $x$, then we could again assume that this torque is spread uniformly [1] across the face of the gripper but in concentric rings. For a circular gripper we would find the maximum moment of friction is $M \le \frac23 \mu NR$ (see Single Friction Disk Clutch). Even for a rectangular or irregular shaped gripper, it would not be difficult to integrate over its surface to find the maximum torque it can supply by friction.

The difficulty comes when trying to combine translational and rotational forces acting on the gripper. We cannot deal with those forces separately because the friction forces which oppose them are not independent, they are coupled : the resultant friction force at each point on the gripper cannot exceed the static limit.

This situation is addressed for sliding friction in Rotational physics of a playing card. It persists for static friction because the direction of friction can still vary from point to point while its magnitude is limited. In the cited article Frictional coupling between sliding and spinning motion the analysis involves elliptic integrals.

This is not an easy problem to solve.

---

Note [1] :

How can friction act uniformly across the gripper if a torque is applied to it? Won't points furthest from the axis bear the most load?

Yes, outer points of the gripper furthest from the axis of rotation would have to supply the most torque at first. This is because microscopically the amount of friction force increases with shear displacement until there is slippage, then it is constant (assuming kinetic friction is the same as static).

Outer points reach the limit of friction first then slip microscopically but continue to supply maximum friction. Inner points progressively closer to the axis gradually reach the limit of friction but slip less. Microscopic slippage continues at each radius inwards until the total friction torque equals the applied torque. Friction has reached maximum at every radius except for a disk at the centre, but this radius will be small if the amount of slippage at maximum static friction is small.

The same mechanism also works when applied forces are not purely rotational. There will be microscopic slippage at some points to enable other points to provide more friction. This continues until either (i) the total friction force equals the applied forces and torques, or (ii) every point has reached the static frictional limit so that no more frictional force or torque can be supplied.

Answer 2

As long as the acting forces do not pass through the barycenter of the object being manipulated, torque of imbalance will arise. These torques will cause turns in the manipulated object as long as the forces of friction and therefore the moment of friction, is not enough to contain the moment generated by the accelerations with which the manipulator moves the object. Therefore it is more a problem of friction.