We know the Brachistochrone problem that to find the shape of the curve down which a bead sliding from rest and accelerated by gravity will slip (without friction) from one point to another in the least time.
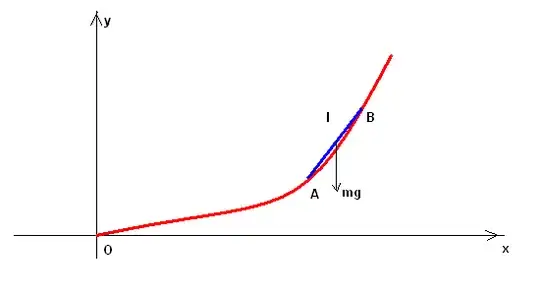
I wonder if we use a line segment mass on a curve with the same problem. It is clear that the line segment mass will touch two point on the curve. Which curve equation must be for the least time in that case? I do not know how to start.
Note: Line segment mass is released from point A and its finish place is origin (O). the line segment mass is homogen and lenght is $l$ and mass is $m$. no friction is in the system.Point $A(x_1,y_1)$ and Point $B(x_2,y_2)$ are given starting points.
Thanks for answers