I have spent some time looking at how to design a field mapping system that turns a Gaussian beam profile into a top-hat beam. However, it would also be very useful to have a very sharp super-Gaussian profile for a different experiment.
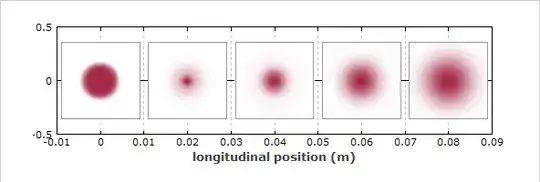
I have found a page (the RP Photonics article on flat-top beams) which argues that since the top-hat is not a free space mode of the Helmholtz equation, the profile changes as it propagates. From the simulated model (Figure 1) and the description given by the author it looks to me like the top-hat might initially collapse to something resembling a super-Gaussian but its a bit hand-wavy to deduce that from an intensity plot.
My question now is: Does anyone have a suggestion as to how to replicate this simulation or at least find a way to solve for the specific intensity profile I am looking for. Which equations do I use and how can I apply them for a computational solution (I'm guessing the solutions will have to be numerically evaluated)?
Or alternatively, is my reasoning just plain wrong and the profile does not contract into a super Gaussian as the beam propagates?