Would current flow through the resistor below?
The power source is an ideal cell without internal resistance, and the wires are also ideal.
I thought that current won't flow through the resistor because there is no potential difference between the points $\text{A}$ and $\text{B}$, but I am not sure.
If the lower wire from A to B is not assumed to be of zero resistance then definitely current would flow through both of them.
If the upper net resistance is $R_\text{upper}$ and the lower is $R_\text{lower}$ then $$ \frac{I_\text{upper}}{I_\text{lower}}~=~\frac{R_\text{lower}}{R_\text{upper}} \,.$$
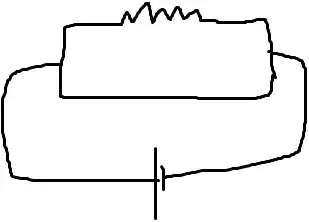
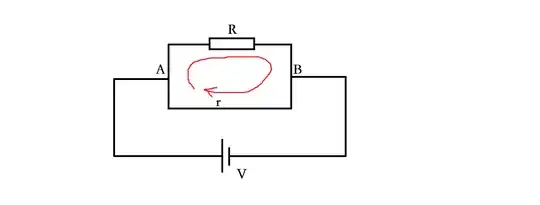
There are a few different loops for this circuit, and it looks like there should be only two independent loops, but I find it helpful to look at three different loops for the "loop rule" to understand what "would happen."
Loop 1 (pass through the battery and along the wire with the resistor and back to the battery): $$ V=IR $$
Loop 2 (go from your point A to point B through the resistor and back to point A via the wire): $$ IR=0 $$
Loop 3 (pass through the battery and along the wire back to the battery): $$ V=0 $$
Seems like such a circuit can't "exist" except when $V=0$, which means $I=0$.
On the other hand, if the wire isn't "perfect" but actually a small finite resistance "r" (through current which $i = I_0 - I$ flows) then the equations are:
Loop 1 (pass through the battery and along the wire with the resistor and back to the battery): $$ V=IR $$
Loop 2 (go from your point A to point B through the resistor and back to point A via the wire): $$ IR=ir $$
Loop 3 (pass through the battery and along the wire back to the battery): $$ V=ir $$
In both sets of equation there are really only two independent equations and we need some more rules, e.g., the junction rule ($I_0=I+i$) and the equivalent resistance rule ($1/R_0 = 1/R + 1/r$), to make much more progress.
If we use the second rule above we can also write: $$ I/i = r/R $$ (as another answer has also stated). In this case it again appears that we can say $I=0$ if $r\to 0$.
But regardless, the main issue is that if you presuppose an ideal wire connected directly between the terminals of a "ideal cell", as in the picture, there is actually no way to sustain a non-zero potential difference across the "ideal cell."
You can also understand this logical problem from the definition of electrical potential. If you have a perfect conductor (the ideal wire) connected from one terminal of a "battery" to another the potential difference across the terminals must actually be zero since the electric field inside a perfect conductor is zero and I can go all the way from one terminal to another inside the perfect conductor:
$$ V = \int E\cdot dl = \int 0 = 0 $$
So, basically, yes, you are correct, the current I is zero. However, this is because the picture cannot make sense unless the ideal cell has $V=0$. It is just absurd otherwise; we can make absurd drawings, we can make absurd statements, we can pose absurd questions. For example, I could ask you: "What is the square root of a hockey puck?" Clearly this is absurd, and really there is no good answer since there is no good question.
The essential problem here is that you haven't specified whether the schematic is an ideal circuit model or not.
If ideal, then you have drawn a contradiction - it is well known (in EE) that an ideal wire across an ideal (non-zero) voltage source results in a contradiction, e.g., $12\,\mathrm{V} = 0\,\mathrm{V}$.
If non-ideal then, to solve this, you must model the non-ideal behavior with additional ideal circuit elements.
For example, if the voltage source has finite short-circuit current $I_{SC}$, you must add an internal resistance $r_S$ in series with the voltage source such that
$$r_S = \frac{V}{I_{SC}}$$
Further, if the wire in parallel with the resistance $R$ is non-ideal, you should add a small resistance $r_w$ in series with the wire. To be sure, you might add additional small resistances in series with the other two connecting wires.
In summary, to properly solve physical circuits (with circuit laws) using ideal circuit elements, you must make sure that you've added the additional ideal circuit elements to account for the non-ideal behavior of physical circuit elements, e.g., physical wires have non-zero resistance, physical voltage sources have finite short-circuit current.
For AC circuits, it's even more complicated as you must also add 'parasitic' inductance and capacitance to account for facts like, e.g., physical capacitors, inductors, and resistors have a Q and a resonance frequency.
We can apply Kirchhoff's loop rule to the small loop containing only the resistor and the wire connecting point A and B, as shown in the following figure.
Assume the current passing the resistor is $I_R$ and the current passing the wire below is $I_r$, then we have $I_R R - I_r r = 0$ since there is no potential source in this loop. (The direction of $I_R$ and $I_r$ are both defined to be from A to B)
Therefore, if the wire below the resistor is ideal, then $r = 0$ and $I_R = \frac{I_r r}{R} = 0$, and no current flow through the resistor. But if we take the resistence of the wire into account, then (this time assume that $R$ is the total resistence of the upper path from A to B) based on the same equation above, there indeed is current flowing through the resistor (although very small, usually undetectable.)
If you're looking for a short answer: yes, the current won't flow. Your argument of no voltage across it is true. IT can also be shown using the intensity for a branch in a parallel of two resistances with $R_2=0$. So yes, ideally, it won't flow. However you will burn the source unless you place any "useful" resistance somewhere.
