Let us imagine some amount of mercury $\left(\text{Hg}\right)$ contained in a cylinder. It is being rotated about the central axis at a constant angular velocity $ω$, and the system has moment of inertia $I$.
I want to find an expression for its radius of curvature. Let us place the cross section of the system on the $\left(x,\,y\right)$-plane such that the $y$-axis passes through the center of the surface and the $x$-axis tangents the surface in the following way:
$\hspace{200px}$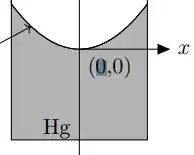 .
.
Now, if we can express this curvature as $y=f\left(x\right)$, then we can say that$$ r=\left| \frac{\left[1+\left(f^{'}\left(x\right)\right)^2 \right]^{3/2}}{f^{''}\left(x\right)} \right| \,.$$
Now, if we can find $f\left(x\right)$ in terms of the $I$ and/or $ω$ and any physical quantity like acceleration due to gravity, we would replace it in the previous equation and find $r$.
Please help me to proceed.
EDIT:
I read the page tagged. My Question is how did the get $y= \dfrac{(x^2 \cdot \omega^2)}{2g}$?