3

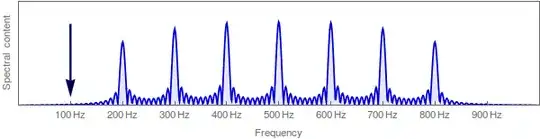
When we pluck a guitar string, we get a wave -- but never a pure sinusoid. Instead, we get a complex superposition of sinusoids, given by the Fourier decomposition (quoting this answer):

$$ y(x,t) = \sum_{k=1}^{\infty} \sin \left(\frac{k\pi x}{\ell} \right) \left( A_k \sin \left( \frac{k \pi c t}{\ell} \right)+ B_k \cos \left( \frac{k \pi c t}{\ell} \right) \right) $$

for string length $\ell$ and wave speed $c$.

My understanding is that where we pluck determines the amplitudes $A_k$ and $B_k$; Fourier analysis tells us those amplitudes, given the initial condition of the pluck shape $y(x,0)$.

But how can we determine the frequency of the complicated function $y$ from the Fourier analysis, i.e. from knowing the $A_k$ and $B_k$? Is the frequency of $y$ just the fundamental frequency $\frac{c}{2\ell}$?

I don't have a guitar handy, so I don't know whether plucking at different positions changes the pitch we hear. Does plucking far up the string give a different pitch than plucking in the middle? If so, then the frequency of $y$ can't always be the fundamental.

josh milligan
  • 159

2 Answers2

3

Generally speaking, if you pluck a guitar string, then the perceived pitch will be independent of the position you pluck it at, and it will be given simply by the usual fundamental frequency $c/2\ell$ as you mention.

What does change is the harmonic content of the emitted sound, i.e. the relative strengths of the different harmonics with respect to each other and to the fundamental, and in human terms this affects the timbre of the sound. Thus, if you pluck near the edge then the sound will have a higher content of higher-order harmonics, which will make the string sound 'harsher' or 'sharper' than the more mellow tone, with lower harmonic content, that you get by plucking at the centre.

However, that said, the human brain is a weird thing, and psychoacoustics is full of surprising phenomena. From a physical perspective, you simply cannot assign a pitch to a sound with multiple harmonics in its spectrum, but the human brain is incredibly effective at assigning perceived pitches in those situations, and particularly if the frequencies present in the sound form a simple harmonic series. On the other hand, that same effectiveness also leads to a bunch of situations where the brain can be fooled into perceiving a pitch that's not actually present (the missing fundamental being a standout example) and other psychoacoustic phenomena that are roughly analogous to optical illusions.

Or, to put this more graphically:

Question: what frequency is this sound?

Mathematica graphics

Physics: There isn't a single frequency. It's a superposition and you can't meaningfully speak of its "pitch".

The human brain: where the arrow is, obviously.

So, you know, tread carefully around perceived pitch. There's some physics in it, but it goes through the human brain and that brain is constantly lying to you about what your senses are actually saying.

Community
  • 1
Emilio Pisanty
  • 137,480
1

When you pluck a guitar string you pull it away from equilibrium. When you release, it is a triangle and where you pluck determines the lengths of the sides. The vibrations are related to the shape of the string by the Fourier Transform. So yes, the overall pitch or strength of various harmonics depend on where you pluck. The energy stored in the string at release has to go somewhere, and how it is distributed among the allowed tones depends on the geometry and the mechanical nature of the string - all the usual properties like tension and such that are used in deriving a wave equation.

C. Towne Springer
  • 1,460