Does entropy increase with a decrease or with an increase in a system’s temperature?

Question

I was trying to understand why in a heat engine there is an increase in entropy. If heat (lower) quality energy is converted to work (higher quality energy), even if not all, why wouldn’t entropy decrease?!

And I got to a website that explained, that is, what I gathered from it was that, high temperature heat (heat from a higher temperature source) had more quality, a higher ability to be turned into work, than heat from a lower temperature source. [I get that it is most likely wrong to state it like this, but it’s the reasoning I made].

And so, high quality heat would come in the machine, some would be turned into work and some other would be turned into a much lower quality heat, so that, the resulting balance would be an increase in entropy. Less from the work exiting the system, but much more from the lower quality heat energy also being transferred from it, resulting in more entropy overall. (Whichever other system work was done on would have its entropy decreased, more mechanical energy, but the surroundings would end up with a much higher entropy, lower quality thermal energy, lower temperature.)

Here’s the picture they have:

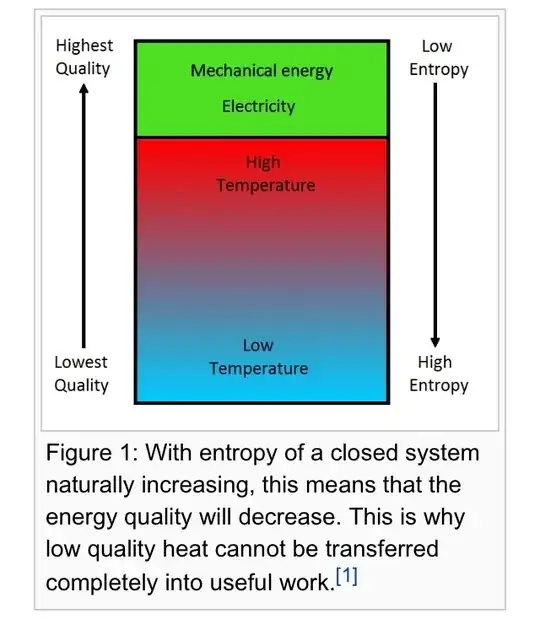
Which made sense to me because at lower temperatures energy is much more “spread” and not so “concentrated”.

But then, I read somewhere else, (and in many other places too, so this must be “where it’s at”, it must be correct) that: “i understand that as temperature increases, entropy increases as well, as there are more quanta of energy and more thermal states(energy levels) available.”

Which also makes sense to me: a macrostate has more entropy if it has a greater number of microstates associated with it. Higher temperature -> more possible energy levels -> more possible microstates -> higher entropy.

So how can I make sense of both things? I get the feeling they are both right in some way and I just don’t know how to connect them. Does entropy increase with a decrease or with an increase in a system’s temperature?

I apologize for the long question and for the, most likely, wrong statements in it. Also, if it would be easy to just “google it by myself”. I have already read some other questions here, but I haven’t understood it yet. Thank you.

References:

To the image: http://energyeducation.ca/encyclopedia/Entropy

To the quote: https://www.physicsforums.com/threads/effect-of-temperature-on-entropy.517807/

Answer 1

Change in entropy is proportional to the reciprocal of temperature. So a lower temperature means less entropy, but higher temperature means less entropy per unit of energy. All else being equal, adding heat to a cold object increases entropy more than adding it to a hot one. Let's say you have a cold reservoir at 100 K and a hot one at 500 K (both have one unit of heat capacity). You extract work, and at the end they're both at 300 K. You started with log(100)+log(500) entropy, and ended with 2log(300), an increase of .255. When you started, most of the heat was in the hot reservoir, where it "counted less" for entropy, and then you moved it to the cold reservoir, where it "counts more" for entropy.

Another way of thinking about it: for energy, it's the sum that matters. But for microstates, it's the product; the total number of microstates for the system involving both reservoirs is not the sum of microstates of the hot and cold reservoirs, but the product: if the cold reservoir has n microstates, and the hot one has m, then there are n*m different combinations of sub-microstates. So if you take away microstates from the hot reservoir, and add them to the cold one, then the total number of microstates increases.

Answer 2

In equilibrium, entropy must be higher for higher temperatures, given fixed values of the other extensive variables describing the state of the system, for example its volume $V$. This happens because of two reasons:

1. Stability requires that the internal energy $U$ be a convex, that is, $\cup$-shaped, function of entropy $S$ and the other extensive variables, say the volume $V$. If it weren't so, the system would never settle into a stable equilibrium state. Mathematically this is expressed by saying that the second partial derivative of the energy with respect to the entropy is not negative: $$\frac{\partial^2 U}{\partial S^2}(S,V) \geqslant 0.$$

2. Temperature is equal to the partial derivative of the internal energy with respect to entropy, keeping the other extensive variables constant: $$T = \frac{\partial U}{\partial S}(S,V).$$

If we combine the two equations above, we find $$\frac{\partial T}{\partial S}(S,V) \geqslant 0.$$ This means that an equilibrium state with higher entropy than another, cannot have lower temperature, given a fixed value of the other extensive variables.

Note that I'm not saying "decreases/increases with", because those verbs give the idea of a process, and for non-equilibrium processes the result above doesn't need to be true, see e.g. https://arxiv.org/abs/1505.06222 or https://doi.org/10.1093/mnras/138.4.495. We're just comparing equilibrium states here.

Note also the important condition "given a fixed value of the other extensive variables". If these are not fixed we can find a state with higher entropy than another but lower temperature – the two states will have different volumes. The entropy for an ideal gas, for example, is higher for higher temperatures and for larger volumes, if we keep the amount of gas constant.

For the result in equilibrium you can see any good book about equilibrium thermodynamics, and I recommend these four works besides:

• A. S. Wightman: Convexity and the notion of equilibrium state in thermodynamics and statistical mechanics, pp. ix–lxxxv in R. B. Israel: Convexity in the Theory of Lattice Gases (Princeton 1979).

• J. W. Gibbs: Graphical methods in the thermodynamics of fluids, Trans. Connecticut Acad. II (1873), pp. 309–342 https://archive.org/details/transactionsconn02conn.

• J. W. Gibbs: A method of geometrical representation of the thermodynamic properties of substances by means of surfaces, Trans. Connecticut Acad. II (1873), pp. 382–404 https://archive.org/details/transactionsconn02conn.

• J. W. Gibbs: On the equilibrium of heterogeneous substances, Trans. Connecticut Acad. III (1875–1878), pp. 108–248, 343–524, 530 https://archive.org/details/transactionsconn03conn.

The last three works are where these concepts about convexity etc. were clearly stated for the first time.

Regarding the non-equilibrium case you can take a look at

• M. Pekař, I. Samohýl: The Thermodynamics of Linear Fluids and Fluid Mixtures (Springer 2014), especially ch. 2.

• G. Astarita: Thermodynamics: An Advanced Textbook for Chemical Engineers (Springer 1990).

The website you consulted seems, to me, very confused and confusing, or it's simplifying things to the point of making wrong statements.