Why are leap seconds needed so often?

Question

In Coordinated Universal Time (UTC), leap seconds are added to account for the slowing down of Earth's rotation. But the slowing down is said to be of the order of milliseconds in a century. Then why there were more than 25 leap seconds added to UTC in the last few decades alone?

Answer 1

It's not the rate of change of the rotation speed that's important, it's the current rotation speed (in the rotating reference frame that stays facing the sun) not matching a 24h day.

Thus leap seconds (on average¹) accumulate at a near-constant rate, because (as you point out) the average rate of change is low compared to the existing mismatch between actual day length and what our clocks say.

Remember that a leap second is an absolute offset added/subtracted, not a multiplier on the speed of our clocks that fixes the problem for the future until the speed drifts some more.

We're correcting the "error" in our time function by adding step offsets, not by changing the slope. The length of an SI second remains fixed, and the length of a day by our clocks remain fixed at 24 hours / 86400 SI seconds (with no leap second).

---

1. In practice the linear model doesn't work at all in the short-term: there's lots of year-to-year variation, and 1.5-2ms/day/century is only a long-term average. See @David Hammen's answer for a nice graph and more details. He commented:

Nine leap seconds were added in the first eight years after implementing the concept of leap seconds while only two were added over the 13 year span starting in 1999.

The chaotic short-term variation dominates over any period short enough to ignore the average slowdown.

---

More details from the US Naval Observatory's Leap Second article

The SI second ($9 192 631 770$ cycles of the Cesium atom) was chosen to be $1 / 31 556 925.9747$ of the year 1900.

The Earth is constantly undergoing a deceleration caused by the braking action of the tides. Through the use of ancient observations of eclipses, it is possible to determine the deceleration of the Earth to be roughly 1.5-2 milliseconds per day per century.

The second that was specified in terms of the mean tropical year of 1900 January 0 was based on the mean solar second computed by Simon Newcomb, using his Tables of the Sun, which used data gathered from 1750 to 1892, and so it corresponds to the mean solar second from around the middle of that period, i.e., ~1820. For further details, see Wikipedia's info on the Ephemeris Second.

Note the units of that measurement: it's ms per day per century, or $\Delta s / s / s$, like an acceleration, not a velocity. And definitely not 1.5 ms per century.

Purely coincidentally, a mean solar day is currently on average 2 ms longer than an SI day, so the current error-accumulation rate is 2 ms / day. It's been a little over two centuries since the defining epoch for the SI second. It takes less than 1000 days to need another leap second. (There are various effects which make solar days differ in length, but on average they're longer than 24h and getting even longer.)

In another century from now (with constant deceleration of the Earth), we'll need to add leap seconds about twice as often as we do now, to maintain the cumulative difference UT1-UTC at less than 0.9 seconds.

Answer 2

It's a cumulative effect. Let's say that the mean solar day is about 1.5 milliseconds longer than the SI day of 86400 seconds. This difference accumulates every single day. After 1000 days, the total difference has become 1.5 seconds. After 18000 days, which is roughly 50 years, the total difference is 27 seconds. This is why 27 leap seconds have been inserted since 1972.

See also this graph on the wiki article about the leap second.

Answer 3

There are good answers here, but there remains a question — if atomic time has only been around for around 50 years, and the Earth's rotation is only slowing at a rate of about 0.5ms / day / century, how is it that we need a leap second every year or two already? Shouldn't we only be accumulating about 1 second of error per decade at this point?

And the answer to that involves a little history: the "atomic" SI second was chosen to maintain continuity with the second of ephemeris time, which was standardized in 1952. And although ephemeris time was based — rather impressively — on over 150 years of astronomical observations, the very length of those observations means that ET reflects the length of the mean solar day in about 1820. As such, the mean solar day was already longer than 86,400 seconds in the 1960s and 1970s by 1-3 ms per day. Which means that when the leap second was introduced in 1972, the error was already accumulating at a rate that required the regular introduction of leap seconds.

In fact, for some of the time since then, the Earth has been bucking the long-term trend and speeding up its rotation, causing the pace of leap second addition to slow down for a time, with none added at all between the end of 1998 and the end of 2005. But this is just a random fluctuation and in the long run, the trend will prevail and the error will grow at an increasing rate, requiring more frequent addition of leap seconds as the centuries roll on, unless some kind of calendar reform makes them unnecessary before then.

Answer 4

Why are leap seconds needed so often?

TL;DR: We need leap seconds somewhat frequently because there's a two hundred year old bias (a non-zero offset) in the definition of a second being 1/86400th of a day.

---

A one thousand word (aka one picture) explanation:

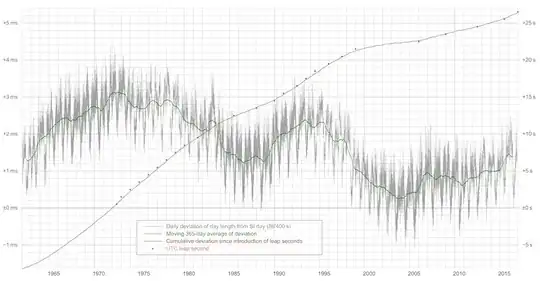
^{Source: Public domain Wikipedia Commons page Deviation of day length from SI day.}

The grey and green curves in the above plot show the variations in the length of day (the length of one mean solar day less 86400 seconds) from 1 January 1962 to 31 December 2016, in units of milliseconds (left vertical axis). The grey curve shows smoothed daily values while the green curve shows a 365 day running average. The red curve shows the area under the curve, with the zero point set at 1 January 1972 (when the leap second concept was introduced). The red dots show when each leap second was introduced. The red curve and red dots are in units of seconds, the right vertical axis.

Note that the length of day exhibits a lot of variability. This short term variability is a result of exchanges of angular momentum between the five differentially rotating parts of the Earth: The atmosphere, the oceans, the crust and mantle, the outer core, and the inner core. What you can't see in this short 55 year span is that length of day also exhibits long term trends. These long term trends are due in part to changes in the Earth's inertia tensor (the Earth is still rebounding from the end of the last ice age) and in part to a secular transfer of angular momentum from the Earth to the Moon.

The transfer of angular momentum from the Earth to the Moon means that a day is now longer than it was in the distant past. While the rate at which the Earth transfers angular momentum to the Moon is very small, this inexorably builds up over time. The day is considerably longer now than it was 4.5 billion years ago (a day is conjectured to have been about four to six hours long shortly after the Moon first formed), and is a good deal longer than it was 2.5 billion years ago (the first reliable observations based on tidal rhythmites).

The day is now also a tiny bit longer than it was a couple of centuries ago. That couple of centuries is key to answering the question "Why are leap seconds needed so often?" Our concept of a day comprising 24 hours, or 86400 seconds, is based on how long a day was a couple of centuries ago. The long term trend makes the Earth rotate a tiny bit slower now than it did back then. This results in a bias (a non-zero offset) in the curve. The bias in the green curve results in the red curve, the area under the green curve, exhibiting a secular growth. Leap seconds are added when the red curve gains a second, more or less.

Detail: The practice is to add or subtract a leap second on June 30 or December 31 when the absolute difference between UT1 and UTC exceeds 0.6 seconds. Leap seconds have always been positive. There has never been a need for a negative leap second due to the ~200 year old bias in the definition of a second.

Answer 5

Earths rotational speed is effected by multiple factors both local to the planet (such as weather) and external (such as solar system gravitational perturbations).

Your questions inherent assumption that only 1 factor influences it and only at 1 constant rate is incorrect.

The speed actually increases and decreases in mathematically chaotic and therefore difficult to predict ways. The IERS attempt to predict changes up to 6 months in advance with the goal of keeping the delta between the highly accurate "atomic time" and civil UTC time below 0.9 SI seconds by adding or removing leap seconds to UTC at the most mathematically and politically appropriate time of year.

Answer 6

A good comparison for this is the US national debt vs. the US national deficit. The US debt is currently about 21 trillion dollars, but the US national deficit for 2017 was less than 700 billion dollars. The leap seconds are like the debt, they keep adding up. The change in the length of day is like change of the deficit, which seems small by comparison to the debt.

Answer 7

Leap seconds are not added to account for the slowing of the Earth's revolution. They are added to account for the fact that the Earth's rotation and its revolution (about the sun) are not perfectly sychronized. Adding an extra day every four years (except for certain unusual circumstances) helps but still does not correct perfectly for the mismatch between rotation and revolution. That is why leap seconds are employed.

Edit: @JBently is correct (see comment below). I did conflate the two different "leap" corrections. Time-keeping is complicated and old memories are sometimes misleading. Jim Garrison also has a point since the day length varies slightly due to weather and geologic factors. Hence the leap second additions are unpredictable.