0

As referred to this question Why can't charge be in a stable equilibrium in electrostatic field?, it is given that

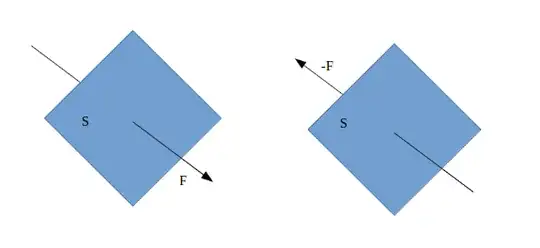
Fig. 5–1.If $P_0$ were a position of stable equilibrium for a positive charge, the electric field everywhere in the neighbourhood would point toward $P_0$. Consider a tiny imaginary surface that encloses $P_0$, as in Fig. 5–1. If the electric field everywhere in the vicinity is pointed toward $P_0$, the surface integral of the normal component is certainly not zero. For the case shown in the figure, the flux through the surface must be a negative number. But Gauss’ law says that the flux of electric field through any surface is proportional to the total charge inside. If there is no charge at $P_0$, the field we have imagined violates Gauss’ law. It is impossible to balance a positive charge in empty space—at a point where there is not some negative charge. A positive charge can be in equilibrium if it is in the middle of a distributed negative charge. Of course, the negative charge distribution would have to be held in place by other than electrical forces.

Please explain the part which is denoted in bold. I have tried to comprehend the idea but did not get anything. My question is why the integral will be negative. I was also reading about this in the book Basic Laws of Electromagnetism, I encountered the same problem where is written:

the flux of E through the surface S is negative

Any help will be appreciated.

Qmechanic
  • 220,844
Chandramauli Chakraborty
  • 105
  • 8

1 Answers1

0

You have to understand that flux is determined by directional quantities. It describes a quantity that passes through an area. Obviously, it will make a difference in which direction the quantity passes through that area.

Consider the following example: You have an arbitrary surface $S$ and a quantity $\vec{F}$ that points through it. You can calculate the flux $\Phi$ by integrating the quantity $\vec{F}$ over the area of the surface $S$. The quantity has a direction and the surface is oriented. You end up with: $\Phi_1 = \int_S \vec{F}\cdot d\vec{A}$

If you now reverse the direction of the quantity, $\vec{F}$ becomes $-\vec{F}$ and you will obtain a minus sign in your flux: $\Phi_2 = -\int_S \vec{F}\cdot d\vec{A}$.

Do you agree that if the flux is non-zero, either $\Phi_1$ or $\Phi_2$ have to be negative? enter image description here

lmr
  • 1,334