17

I know that seasons are caused by the Earth's axial tilt - in summer, latitudes away from the equator receive more surface irradiance (power per unit area), and vice versa in the winter, because of the closer-to-normal incident angle of the sun's rays (it's higher in the sky). It's now spring at my latitude, and I'm starting to feel the "beat" of the sun again - the heat on my skin and clothes caused by the infrared radiation from the sun.

But I started to wonder why I don't feel as much heat on my body and clothes during the winter. Even if the sun is lower in the sky, I can still stand in such a way that my shirt is perpendicular to the direction of the sun, which should maximize the irradiance on my shirt. In fact if I'm walking along, my chest is closer to perpendicular when the sun is lower in the sky - so shouldn't I feel more infrared heating in the winter than in the summer?

Is there something atmospheric going on - like the fact that when the sun is lower in the sky the radiation is traveling through much more atmosphere before it gets to me? Or am I missing something else entirely? Or is it just a sensory illusion caused by the fact that the ambient air is cooler in the winter, making the infrared heating less noticeable?

Zach Saucier
  • 1,191
TypeIA
  • 318

1 Answers1

29

Your question actually contains a half-complete answer :)

like the fact that when the sun is lower in the sky the radiation is traveling through much more atmosphere before it gets to me

Has place, of course. In astronomy, this is called "Air Mass".

This gorgeous pic will illustrate it (with a certain degree of exaggeration of the actual angle with the normal vector for the Earth surface)

Note: Skip to the end of the answer to see the actual data

The gases in the atmosphere absorb the infrared radiation thus dissipating the incoming heat. To see how much role does atmosphere play when it comes to stabilising the heat, you could consider a close example without the atmosphere - the moon. It's said that the temperature of its surface can heat up to >$100^{\circ}$ C, as well as fall to extremely low temperatures.

The atmosphere is also good at scattering the radiation, and the scattering rate is greater for the shorter waves.

You can actually observe the scattering effect yourself - the sky is blue, since the violet colors (smaller wavelength) are being scattered more than the red colors (greater wavelength).

As an example of the lower atmosphere layers plaing a good role, you could consider being on a mountain - despite the fact it's not really significantly higher above the "flat" ground level, the sun here is really more intense, while the temperature is lower (I have been up in the mountains and I know that weird feeling).

As for the illusion, I believe that if anything, it's about the thermoregulation of the body. I think that an example of you hot bathing and then going out to the cold weather - you aren't noticing the fact it's cold outside for a while; i.e. not really dependant on the actual radiation here.

The other fact is not so season-related, but the humidity also having effect; covered here - Why is the sun brighter in Australia compared to parts of Asia?

Let's do some math now with the actual data (thanks @Travis for the data).

The radius of Earth is approx. $6371$ km. The "end" of the atmosphere we'll pick at the height of 100 km (see Kármán line). Note that those numbers are not really relevant, since we're going to get the ratio of length of the path the radiation is going in the winter and in the summer.

I.e., we'll get the answer in the form of $~\dfrac{winter~path}{summer~path}$.

The data is: in the summer the sun was 7.5 degrees from overhead and in the winter the sun was 30 degrees from overhead. Here's how it would look:

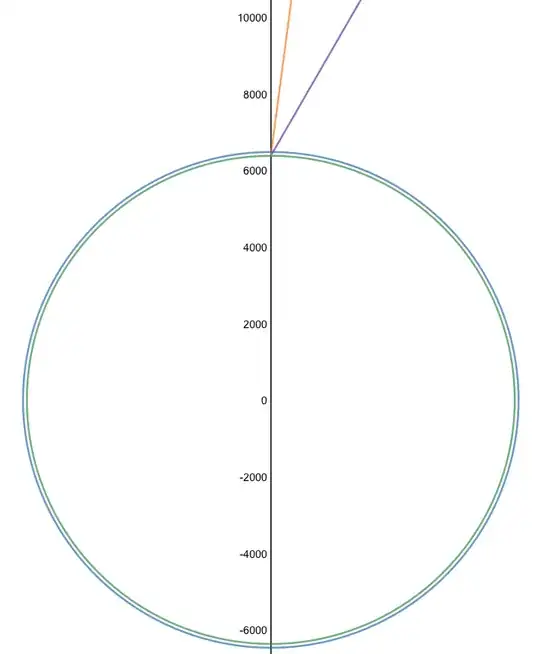
Now let's apply 200x scale and do the analysis:

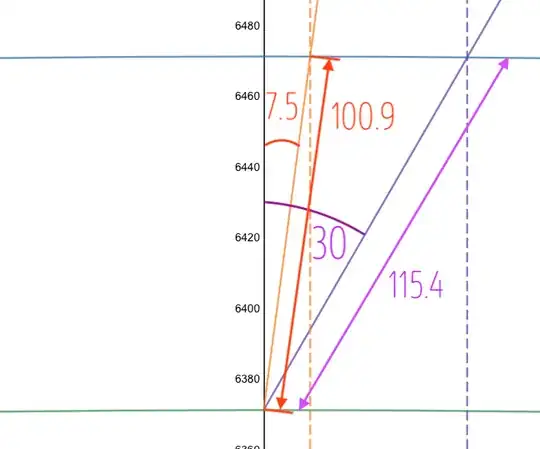
The ratio would be: $\dfrac{115.4}{100.9}=1.144$.

That means, in the winter sun the radiation is going a path longer by 14.4%.

nicael
  • 1,978