Feynman's Lost Lecture: what is the significance of $\frac{d\mathfrak{v}}{d\theta}=-\frac{GMm}{\left|\mathfrak{L}\right|}\hat{\mathfrak{r}}?$

Question

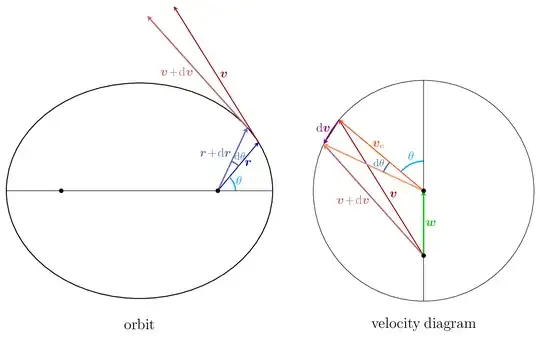
My question pertains to a fact used by Richard Feynman in his so-called Lost Lecture. http://books.wwnorton.com/books/Feynmans-Lost-Lecture/. I have only skimmed the book, so I have much more to learn from it. One of the important insights in Feynman's modified version of Newton's derivation of Kepler's Laws is that the change in the velocity vector per change in polar angle is of constant magnitude and directed parallel to the force.

The following is not Feynman's demonstration of this fact, which did not use calculus. It is my demonstration using calculus. The introduction of the areal velocity is not necessary for the final result. It is included with the hope that it may motivate understanding.

Notation:

$m:$ constant mass of planet.

$M:$ constant mass of (immovable) Sun.

$\hat{\mathfrak{r}}:$ unit vector directed from Sun to the planet.

$\theta:$ polar angle of $\hat{\mathfrak{r}}$, measured in the orbital plane.

$\hat{\mathfrak{k}}:$ unit vector normal to the orbital plane.

$\omega\hat{\mathfrak{k}}\equiv\frac{d\theta}{dt}\hat{\mathfrak{k}}:$ angular velocity of $\hat{\mathfrak{r}}$.

$\hat{\theta}\equiv\frac{d\hat{\mathfrak{r}}}{d\theta}:$ unit vector perpendicular to $\hat{\mathfrak{r}}$ and lying in the orbital plane.

$\mathfrak{r}\equiv r\hat{\mathfrak{r}}:$ radial position of the planet relative to Sun.

$\mathfrak{v}_{\parallel}:$ planet's velocity component parallel to $\hat{\mathfrak{r}}$.

$\mathfrak{v}_{\perp}:$ planet's velocity component perpendicular to $\hat{\mathfrak{r}}$.

$\mathfrak{v}\equiv\frac{d\mathfrak{r}}{dt}=\frac{dr}{dt}\hat{\mathfrak{r}}+r\frac{d\theta}{dt}\hat{\theta}=\mathfrak{v}_{\parallel}+\mathfrak{v}_{\perp}:$ velocity the of planet.

$\mathfrak{p}\equiv m\mathfrak{v}:$ momentum of the planet.

$\mathfrak{L}\equiv\mathfrak{r}\times\mathfrak{p}:$ angular momentum of thee planet.

$\vec{\mathscr{L}}\equiv\frac{\mathfrak{L}}{m}=\mathfrak{r}\times\mathfrak{v}=\mathscr{L}\hat{\mathfrak{k}}:$ angular momentum of a unit mass in the planet's orbit.

$\mathfrak{A}_{\theta}\equiv A_{\theta}\hat{\mathfrak{k}}:$ oriented area of the region enclosed by the planet's radial vector with polar angle $\theta_{0}=0$, the radial vector with polar angle $\theta<2\pi,$ and the path of the planet between those points.

$\mathfrak{a}\equiv\frac{d\mathfrak{v}}{dt}:$ acceleration of the planet toward Sun.

$\mathfrak{F}\equiv-\frac{GMm}{r^{2}}\hat{\mathfrak{r}}=m\mathfrak{a}:$ gravitational force of Sun on the planet.

Demonstration:

Angular momentum is a conserved geometric object

$$ \frac{d\mathfrak{L}}{dt}=\mathfrak{0}. $$

The parallelogram associated with the cross product gives

$$ \mathfrak{r}\times d\mathfrak{r}=2d\mathfrak{A}_{\theta}. $$

This is related the the unit mass angular momentum

$$ \mathfrak{r}\times\frac{d\mathfrak{r}}{dt}=2\frac{d\mathfrak{A}_{\theta}}{dt}=\vec{\mathscr{L}} $$

$$ =\mathfrak{r}\times\left(\mathfrak{v}_{\parallel}+\mathfrak{v}_{\perp}\right) $$

$$ =r\hat{\mathfrak{r}}\times r\frac{d\theta}{dt}\hat{\theta} $$

$$ =r^{2}\frac{d\theta}{dt}\hat{\mathfrak{k}}. $$

It follows that the distance and angular speed are related to the constant magnitude of angular momentum by

$$ \mathscr{L}=r^{2}\frac{d\theta}{dt}. $$

Rewriting this result gives

$$ \frac{1}{r^{2}}=\frac{1}{\mathscr{L}}\frac{d\theta}{dt}. $$

Substituting this into the force equation gives

$$ \frac{d\mathfrak{v}}{dt}=-\frac{GM}{\mathscr{L}}\frac{d\theta}{dt}\hat{\mathfrak{r}.} $$

A simple manipulation shows that the derivative of velocity with respect to the polar angle is of constant magnitude with the same sense and direction as the gravitational force acting on the planet.

$$ \frac{d\mathfrak{v}}{d\theta}=-\frac{GM}{\mathscr{L}}\hat{\mathfrak{r}} $$

$$ =-\frac{GMm}{\left|\mathfrak{L}\right|}\hat{\mathfrak{r}}. $$ Written in terms of force

$$ \frac{\mathfrak{F}}{\omega}=\frac{1}{\omega}\frac{d\mathfrak{p}}{dt}=-\frac{GMm}{\mathscr{L}}\hat{\mathfrak{r}}. $$

Question: Is this relationship associated with some specific conservation law, or with some stationary value such as "action"?

Is there any other valuable insight to be had from this relationship?

Answer 1

Forgive me if I'm going to use my own notations. Using the polar unit vectors

\begin{align} \boldsymbol{e}_r &= \cos\theta \boldsymbol{e}_x + \sin\theta \boldsymbol{e}_y,\\ \boldsymbol{e}_\theta &= -\sin\theta \boldsymbol{e}_x + \cos\theta \boldsymbol{e}_y, \end{align}

we find

\begin{align} \boldsymbol{r} &= r\boldsymbol{e}_r,\\ \boldsymbol{v} &= \dot{r}\boldsymbol{e}_r + r\dot{\theta}\boldsymbol{e}_\theta = \dot{r}\boldsymbol{e}_r + \boldsymbol{\omega} \times \boldsymbol{r},\tag{1} \end{align}

with $\boldsymbol{\omega} = \dot{\theta}\boldsymbol{e}_z$. Let's also define the specific angular momentum $\boldsymbol{h}$ as \begin{equation} \boldsymbol{h} = \boldsymbol{r} \times \boldsymbol{v} = r^2\boldsymbol{\omega}, \end{equation} so that $h = r^2\dot{\theta}$.

The acceleration $\boldsymbol{a}$ is given by

\begin{equation} \boldsymbol{a} = -\frac{\mu}{r^2}\boldsymbol{e}_r, \end{equation}

which can be written as

\begin{equation} \boldsymbol{a} = -\frac{\mu}{h}\dot{\theta}\boldsymbol{e}_r = \frac{\mu}{h}\dot{\boldsymbol{e}}_\theta= \boldsymbol{\omega} \times \boldsymbol{v}_\text{c},\tag{2} \end{equation}

with

\begin{equation} \boldsymbol{v}_\text{c} = \frac{\mu}{h}\boldsymbol{e}_\theta. \end{equation}

This is equivalent with the equation you derived:

\begin{equation} \frac{\text{d}\boldsymbol{v}}{\text{d}\theta} = -\frac{\mu}{h}\boldsymbol{e}_r. \end{equation}

The significance of this equation is the cornerstone of Feynman's proof, namely that the velocity diagram of a Kepler orbit is a circle. Indeed, integrating Eq. $(2)$ yields

\begin{equation} \boldsymbol{v} = \frac{\mu}{h}\boldsymbol{e}_\theta + \boldsymbol{w} = \boldsymbol{v}_\text{c} + \boldsymbol{w},\tag{3} \end{equation}

where $\boldsymbol{w}$ is a constant vector. Without loss of generality, we can orientate the $(x,y)$ coordinate axes such that $\boldsymbol{w} = (0,w)$, so that

$$ v_x = -v_\text{c}\sin\theta,\qquad v_y-w = v_\text{c}\cos\theta, $$ which is indeed the equation of a circle, with radius $v_\text{c}$. And because $\boldsymbol{w}$ is constant, we do have an additional conservation law. The diagrams below illustrate this further:

Eq. $(3)$ actually provides us with an elegant method to derive $r(\theta)$. We can combine Eqs. $(1)$ and $(3)$ to get an expression for $\boldsymbol{w}$:

\begin{align} \boldsymbol{w} &= \boldsymbol{v} - \frac{\mu}{h}\boldsymbol{e}_\theta = \dot{r}\boldsymbol{e}_r + \left(r\dot{\theta} - \frac{\mu}{h}\right)\boldsymbol{e}_\theta = \dot{r}\boldsymbol{e}_r + \left(\frac{h}{r} - \frac{\mu}{h}\right)\boldsymbol{e}_\theta. \end{align}

Multiplying $\boldsymbol{w}$ by $\boldsymbol{e}_x$ and $\boldsymbol{e}_y$ respectively, we obtain

\begin{align} \dot{r}\cos\theta - \left(\frac{h}{r} - \frac{\mu}{h}\right)\sin\theta &= 0, \\ \dot{r}\sin\theta + \left(\frac{h}{r} - \frac{\mu}{h}\right)\cos\theta &= w. \end{align} Multiplying these equations by $\sin\theta$ and $\cos\theta$ respectively, and subtracting them, we get

\begin{equation} \frac{h}{r} - \frac{\mu}{h} = w\cos\theta, \end{equation}

or \begin{equation} r = \frac{h^2/\mu}{1 + e\cos\theta}, \end{equation}

with $e = h w /\mu$ the orbital eccentricity.

It also follows that

\begin{equation} \boldsymbol{v} = \frac{\mu}{h}\left(\boldsymbol{e}_\theta + e\boldsymbol{e}_y\right), \end{equation}

which means that $\boldsymbol{v} = \boldsymbol{v}_\text{c}$ for circular orbits. The conservation law associated with $\boldsymbol{w}$ is more commonly expressed in terms of the Laplace-Runge-Lenz vector: \begin{equation} \boldsymbol{A} = m^2(\boldsymbol{w} \times \boldsymbol{h}). \end{equation}

For more information on the symmetry associated with this vector, see this post.