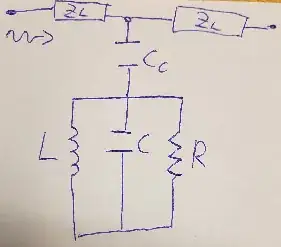
I have an inductor coupled via coupling capacitance $C_c$ to a transmission line (waveguide, feedline?) with impedance $Z_L$. Given that the inductor has some internal losses and a capacitance, I imagine that for all intents and purposes it can be modeled as an RLC circuit. This gives a simple circuit shown below:
Here I have to admit that putting the resistance in series might actually make sense instead, I'm a bit stuck on that mentally; the losses originate from losses in the superconducting that makes up the inductor. However, what I am interested in here is an analytic expression for the external quality factor $Q_E$ of the circuit in terms of $C_c$, $C$, $L$, $Z_L$, and perhaps $R$ but I imagine that only goes into the internal quality factor regardless of how we put it in.
Now, from the definition of the quality factor, we can write that $$Q_E = \omega \frac{E}{P}$$
where $\omega$ is the frequency, $E$ is the energy stored in the RLC circuit, and P is the power lost in the transmission line, essentially due to the coupling. But I have to admit, at this point I'm already starting to get stuck in relating it to the circuit parameters; my circuit analysis is definitely somewhat rusty beyond $E = 1/2 CV^2$, $E = 1/2 LI^2$ and $P = V^2/R$.
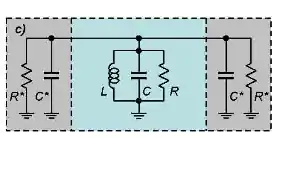
Coplanar Waveguide Resonators for Circuit Quantum Electrodynamics by Goppl et al from 2008 does look at a circuit along these lines, but this is not an identical system. They transform their circuit using Norton equivalences (I have to admit I can't follow this step all that well, not familiar with the equivalence in this context). If one were to take their figure 5c and make some adjustments, perhaps that helps?
Taking the above with $R* = R_L$, $C* = 0$, and replacing $C \rightarrow \frac{C_c C}{C_c + C}$, would that not be identical? In that case the external quality factor is given in the paper to be \begin{equation} Q_E = \frac{Z_L}{2} \frac{C_c C}{C_c + C}\omega_0 \end{equation} where $\omega_0$ is then the resonant frequency of the circuit taking into account the coupling capacitance. I am not 100% sure this is correct; could someone help me out there?