How does the orbiting of electrons around nuclei START?

Question

When electrons orbit a nucleus, their orbiting continues due to conservation of angular momentum, so I've read. But what causes an electron to orbit a nucleus in the first place? To be more precise, what happens exactly when an atom absorbs an electron?

Answer 1

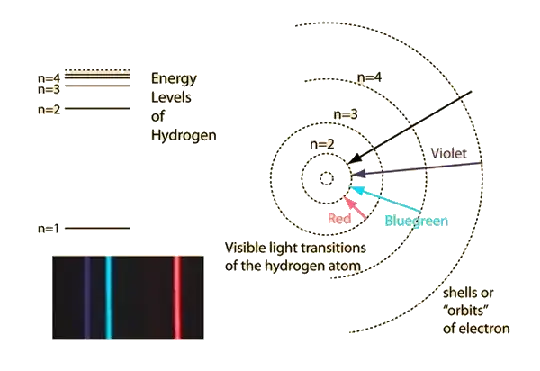
You are describing the Bohr model of the atom, which was able to fit the spectra observed from excited atoms, the lines seen in the hydrogen atom:

In order to explain why the orbits could be stable instead of spiraling down to the nucleus as classical electrodynamics would expect, the model assumes quantization of angular momentum to succeed at a stable atom.

This was a hypothesis that partially fitted the hydrogen atom, and got more impossible for complex nuclei.

Quantum mechanics , as it evolved from the simple solutions of the Schrodinger equation, managed not only to reproduce the partial success in the series solutions for the hydrogen atom, but also to develop into a theory with a much wider scope, which describes all nature at the underlying particle level.

In the quantum mechanical system, there are no orbits, there are solutions of the potential problem which give the probability of finding the electron at an (x,y,z) if one tried to measure its position. These loci are called orbitals. Here are the orbitals calculated for the hydrogen atom:

for the different quantum numbers that characterize the electron occupation of an energy level.

Here is a first experiment that looks at these orbitals:

To be more precise, what happens exactly when an atom absorbs an electron?

Precision needs quantum mechanics.

The electron falls into the potential well of the atom, radiating a photon which carries off angular momentum so that conservation of angular momentum is satisfied, and gets bound in an energy level. If lower energy levels are empty, it will cascade down with more radiation, to the last unfilled energy level.

Answer 2

At some point in the early history of the universe, protons had to capture free electrons to form neutral hydrogen, but $pe\to H^*$ violates conservation of energy and/or momentum, so it has to be something like $pe\to H^*\gamma $. Any charged bystander (say another nearby proton) could take up the extra momentum, so $ppe\to pH^*$ is also allowed. The asterisk means excited -- not in the ground state. Ordinarily, when an electron is captured, the newborn atom is in a quantum state of high angular momentum, close to the angular momentum predicted by classical mechanics. The excited atom then gives up energy and angular momentum via a sequence of radiative transitions, emitting a photon at each step, until it lands in its ground state.

Answer 3

The problem I found in this problem is that the questioner is sticking to the old idea that electron is a particle and it got a well defined path (since it orbits around the nucleus). QM prohibits this idea in the first place ( you can't even think of path in the first place). The second point what happens when electron gets absorbed by atom can be thought same as what happens when particle is introduced in a infinite potential well though the case are a bit different in the latter one the question arises how you got the particle inside the well in first place. While in former one the potential reaches up to infinity so no drama over it's existence in first place . Since you are talking about the electron in first place you have to give me it's initial wavefunction and that's the deal to use Schrodinger's equation. Now take the case of hydrogen atom( cause that's what I only know nothing about multi-electron atom) and since we know it's eigenfunction ( radial and spherical harmonic) and they are complete ( they can span whatever you want) so I will decompose initial given wavefunction in terms of this basis and I will be done to tell you about future prediction (only statistically). So we can't just say what happens to electron you really need to tell me it's initial wavefunction. Take a look at Ex. 2.2 Griffiths QM. Further refinement will be given by QFT.

Answer 4

Normally physicists use a limited set of equations to describe the specific situation of an electron orbiting a nucleus, i.e. an electron trapped in a potential well. They might use something simple like the time independent Shrödinger equation for simple systems, or something more realistic like Dirac's equation to examine relativistic effects, which lead to things like antiparticles and magnetism. However all these equations describe the situation of an electron stuck in a potential well, not things like ionization or the motion of free electrons that become captured.

For those situations you really need the full quantum field theory of quantum electrodynamics. This describes the electron and photon field and includes such things as creation and annihilation of particles and particle interactions and motions through extended space. The quantum field theories can include any number of particles existing at the same time and moving every which way, and interacting with virtual particles in the vacuum.

However the simple models are normally used in physics or chemistry on a day to day basis and they have well known solutions for common cases.

Solving QED or the full Lagrangian of the standard model of physics, even for very simple systems is very hard. However these advanced field theory models can show precisely how wave functions for the electrons and other particles interact over time during something like electron capture.

Edited, because of comments below.

However I believe the original poster is particularly asking about the description of electron capture, not steady state orbits, and I wanted to point out that to show exactly what happens requires more than a description using steady state orbital equations. As another poster has said, the electron falls down through a cascade of energy levels with photons emitted at each transition. But since the electron can come in from infinity from any direction there is the question of what happens to the original linear momentum, and I was trying to say in the original deleted point, that linear momentum is interpretable as angular momentum around the center of the atom, even when the electron is far away.

Answer 5

But what causes an electron to orbit a nucleus in the first place?

Nothing. At least not in the sense you're asking. Let's explore this with a classical example.

Consider an asteroid moving through empty space. It has some trajectory and some mass, so we can calculate its momentum.

Ok, now let's consider that same asteroid in orbit around Jupiter. Now it also has an angular momentum, it's orbital angular momentum, which is a sort of made-up value from it's trajectory and distance from Jupiter.

Ok, now imagine the case where the asteroid is flying by Jupiter. Maybe it's going fast enough that it just keeps on going, like most comets. But maybe it ends up in just the right place at the right time with just the right speed and it begins orbiting, like the Trojans.

So what "happened" to make it "began orbiting". Nothing! Jupiter's gravity is pulling on it all along, nothing changed.

what happens exactly when an atom absorbs an electron

It doesn't! If there's an electron going on it's merry way that just happens to have the right trajectory (for lack of a better word) then it will start "orbiting". If it doesn't, it will keep going, on some modified trajectory. Nothing "happens" when it enters orbit, it's the exact same physics it experienced when it didn't enter orbit, or when it was far away from the atom and never even noticed it.

There are major differences between the physics of the two cases. For instance, in the case of the asteroid, it's "internal" spin has no effect, but that is not the case for the electron. But from a high level, they're pretty similar.