How does one calculate the stability of a ring cavity?

Question

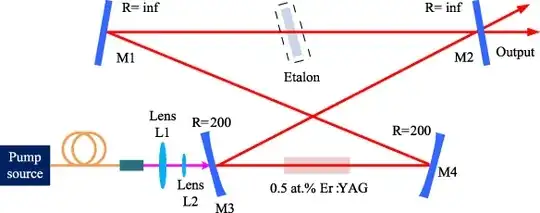
When discussing whether or not a cavity is stable, i.e., if a beam stays inside the cavity, one can either employ the ABCD-matrix approach, in which case the cavity is stable if $$ 0 \leq \frac{A+D+2}{4} \leq 1 $$ In a cavity with two perfectly parallel planar mirrors, for example, $A=D=1$, and the relation holds. Another approach, when using curved mirrors, is to define $$ g_1 = 1 - \frac{L}{R_1}, \quad g_2 = 1- \frac{L}{R_2} $$ where $L$ is the optical path length in the cavity and $R_i$ the radii of the curved mirrors (negative if the mirror is concave). Stability is then given if $$ 0 \leq g_1 g_2 \leq 1 $$ Now, my question: which approach, if any of those two, would I use if I had a ring resonator, specifically a bow-tie type cavity?

There are 4 mirrors here, 2 curved and 2 planar, and some other elements like Brewster windows or an etalon. Is there e.g. some numerical approach I could calculate with Mathematica or similar?

Answer 1

The general approach is that the magnitudes of the eigenvalues of the transfer matrix of the ring round trip must both be below unity. This translates to the physical statement that the beam width at any given point along the cavity shrinks with each round trip, i.e. that the whole beam stays within the cavity. If either of the eigenvalues exceeds unity, a few bounces put the beam outside the cavity, thus abruptly quenching the resonance.

The first criterion expresses this idea. The second criterion you cite is a special case of the first for the case of two spherical mirrors of curvature radiusses $R_1,\,R_2$ spaced by an on-optical-axis distance of $L$ each way.

The eigenvalues of the transfer matrix (or any $2\times2$ matrix) $M$ are:

$$\lambda = \frac{1}{2}\left(\mathrm{tr}(M)\pm\sqrt{\mathrm{tr}(M)^2-4\det(M)}\right)$$

but transfer matrices are always symplectic so in particular must have unit determinant. This leads to the first inequality you cite.

Now calculate the transfer matrix for the round trip for the spherical mirrors. You will find that the $g_1\,g_2$ quantity is equivalent to $\frac{1}{2}+\frac{1}{4}\mathrm{tr}(M)$.

So, obviously, you will use the first criterion for the transfer matrix of the round trip in your setup.