Why is the hypersphere not seriously considered by cosmologists as the best model for the overall shape of the universe?

Question

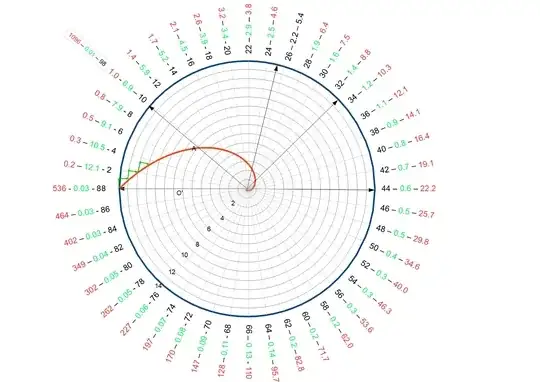
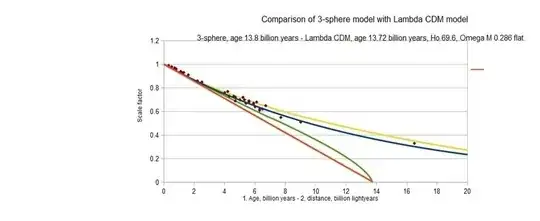
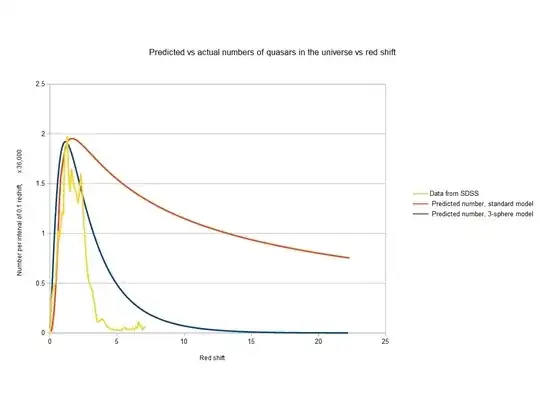
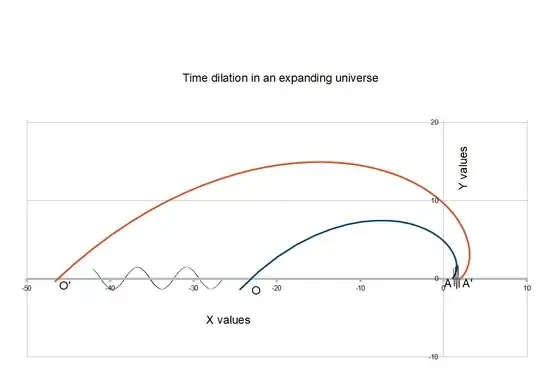
Cosmologists seem to not seriously consider the hypersphere as the best model for the universe even though they mention it as a candidate from time to time. If you look closely, it seems to be a very good fit.

The surface of a hypersphere is 3D and unbounded, just like our universe. And if one assumes the radius of the hypersphere is 13,820 Million Light-Years, and is increasing at the speed of light then one can calculate the expansion rate of the universe (which we all know as Hubble's constant). It would be the speed that the circumference of the hypersphere is increasing (2 pi c) divided by the length of the circumference of the hypersphere (2 pi R). So it would be (2 pi c)/(2 pi R) or (c/R).

Plugging in the numbers one gets 21,693 m/s/Mly, and after multiplying by 3.2615 to convert to mega-parsecs and dividing by 1,000 to convert to kilometers one gets 70.75 km/s/Mpc (which are the units for Hubble's constant astronomers like to use). The currently accepted value of Hubble's constant is around 71 km/s/Mpc.

So the hypersphere model fits the facts very well, but cosmologists do not embrace the model. What are the objections of the cosmologists to the hypersphere model of the universe? What facts or observations does the hypersphere model not fit?

Answer 1

Why is the hypersphere not seriously considered by cosmologists as a model for the overall shape of the universe?

This is simply not true.

FLRW models are the most important models used by cosmologists, and they come in two flavors, open and closed (plus a borderline case, which is flat). The closed type has spatial cross-sections that are hyperspheres. If we fit parameters to a variety of cosmological observations, the universe is constrained to be very nearly spatially flat, but the error bars on the spatial curvature are big enough to allow both open and closed cosmologies. Therefore a hypersphere is currently a perfectly reasonable candidate for the spatial geometry of our universe, and cosmologists do take it seriously.

If this is the geometry, then models that fit the data constrain the radius of the hypersphere to be very large (IIRC orders of magnitude greater than the radius of the observable universe).

And if one assumes the radius of the hypersphere is 13,820 Million Light-Years, and is increasing at the speed of light then one can calculate the expansion rate of the universe (which we all know as Hubble's constant). It would be the speed that the circumference of the hypersphere is increasing (2 pi c) divided by the length of the circumference of the hypersphere (2 pi R).

Here you seem to be mixing up the observable universe with the entire universe. Even if we're talking about the observable universe, it doesn't expand at c.

Answer 2

If you look closely, it seems to be a very good fit.

You didn't look closely, though – you only calculated one parameter from your model. If you calculate more, you'll find that the rest of them don't fit.

if one assumes the radius of the hypersphere is 13,820 Million Light-Years [...] one gets 70.75 km/s/Mpc

That value is just 1/(13820 million years) in km/s/Mpc.

It's true that the current value of the Hubble parameter is close to the reciprocal of the current age of the universe, but it's just an accident of the era we live in, like the Sun and the Moon having the same angular size. In this diagram, your model's prediction is the solid line labeled $\Omega_M = 0$, while the curve consistent with observations is the dashed one labeled $\Omega_M = 0.3, \Omega_\Lambda = 0.7$. They're normalized so they have the same zeroth and first derivatives at t=now, and they intersect the x axis at almost the same place – that's the coincidence. If you normalize them to match at any time significantly different from now, the x intercepts will be much farther apart.

Your model is also inconsistent with general relativity, although a similar model with a hyperbolic space instead of a sphere is consistent with GR (that's the $\Omega_M = 0$ model in that diagram).

There's nothing really wrong with your idea in principle, and it resembles cosmologies others have invented in the past, but it's very strongly excluded by current observations.

Answer 3

I am certain our universe is a 3-sphere (hypersphere if you prefer. It explains far more than has been presented here so far. But first we need to deal with the idea that fluctuations in the CMB prove the universe is flat. The argument centres on the idea that fluctuations in the universe are growing at the speed of light up until the period of recombination, around 300,000 years. But this age is specific to the standard model, already assumed to be flat. To use it in this way leads to a circular argument. In fact in the simplest 3-sphere model, recombination occurs at an age of around 13 million years.

Here are other predictions of the simplest 3-sphere model.

1. The age of the universe is the reciprocal of the Hubble constant.

2. Here is how light travels around a 3-sphere universe, forming a logarithmic spiral.

This leads to the following image where scale factor vs distance and scale factor vs time are compared between the 3-sphere model and the standard model also showing the data of Perlmutter et al. Up to a redshift of around 11, the redshift vs distance is almost identical in the two models, but the ages of the very early universe are significantly greater, very welcome to those who study galaxy formation. Incidentally, the 3-sphere universe requires neither dark energy nor inflation. The requirement for dark matter is the same as in the standard model.

3. The density of this 3-sphere universee is equal to the FLRW critical density.

4. The mass of this universe is proportional to its radius, just like a black hole. Einstein originally thought the universe was a 3-sphere, but I suspect this may have been his sticking point.

5. Exactly 50% of this universe is gravitational potential energy, which is negative, leading to a universe consisting at all times of zero total energy.

6. There is an incredibly simple calculation, involving the area of the 3-sphere, which results in a value of -1/3 for the equation of state.

7. The 3-sphere model predicts the number of objects we see as we look deeper into space, far better than the standard model. This is shown for quasars using data from the Sloane Digital Sky Survey

8. In the 3-sphere model, the time dilation of special relativity is a simple application of Pythagoras.

9. Cosmological redshift is explained by the following diagram. You can see the redshift occuring before your eyes.

The paths of light, which are geodesics become increasingly tightly curved as the centre of this universe is approached, indicating that the force of gravity is increasing. This is gravitaional time dilation. The numbers support this beautifully.

10. This 3-sphere universe is identical in all of its major aspects to the FLRW curvature-only universe. This latter is commonly thought to be empty, but of course, if the energies of its components sum to zero, they will not affect the metric.

11. It has been countered that the FLRW curvature only universe must be hyperbolic. But take a look at the diagram below. It can be seen that a hyperbolic space has an internal boundary which is a sphere of positive curvature.Hyperbolic spacetime can still have a 3-sphere boundary.