If I drop a ball in an accelerating rocket, will it bounce? If so, how?

Question

Einstein's equivalence principle says that you cannot distinguish between an accelerating frame or a gravitational field. However, in an gravitational field, if I drop a tennis ball, it will bounce, but I don't think that it will in the accelerated rocket. Will it bounce? If so, how?

Answer 1

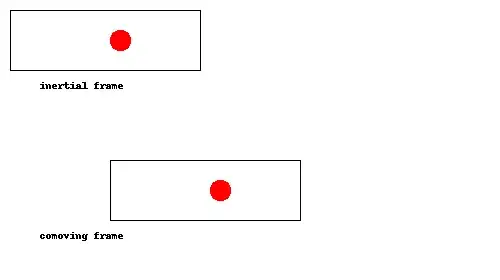
This is one of those things that should become clear once you see it, so I made an animation:

As you can see, the ball simply bounces off the back of the rocket once the rocket catches up with it, just like a tennis ball bouncing off the racket during a serve. In the comoving frame (i.e. if we are accelerating along with the rocket), this amounts to the ball bouncing off the floor.

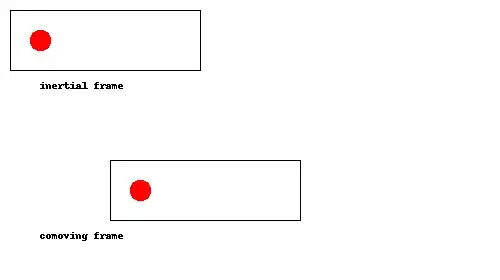
Since the rocket is still accelerating but the ball is not, the rocket will eventually catch up with the ball again and it will bounce a second time. Here is a bonus animation showing multiple bounces:

In this version the ball bounces elastically, and it starts at a lower height, so that several bounces can be observed before the rocket reaches the side of the image. It's a little hard for the eye to see, but in between collisions the ball moves at a constant speed, while the rocket accelerates to catch up with it.

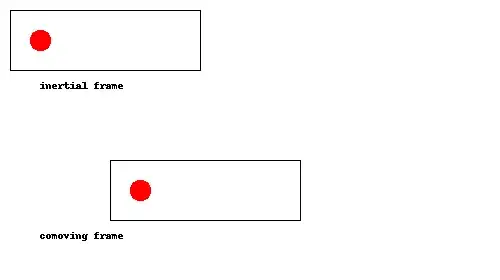
Finally, here's another bonus animation to show that if the ball doesn't bounce elastically then it will stop bouncing and start just moving along with the rocket:

Answer 2

The ball will bounce exactly as it would on the surface of a planet with local gravitational acceleration equal to the rocket's acceleration.

The physics really does play out exactly as in Einstein's accelerating rocket thought experiment, and not even bouncing balls will tell the accelerating frame apart from a planet's surface for you in this regard.

I suggest that you work the problem out from a inertial frame removed from the rocket. You let the ball go, and then the floor of the rocket accelerates towards the ball whilst the ball coasts with the velocity it has at the instant of release. Calculate the effects of collision from there, and then transform the ball's position versus time path back to the accelerated co-ordinates; you will find my first two paragraphs to be true.

Answer 3

Let's say both the rocket and the ball start at zero velocity and the rocket accelerates at a constant rate.

The ball starts at some distance $s$ from the floor.

In the time it takes for the rocket to travel $s$ (the first bounce), it will have accelerated to a certain speed, $v$ let's say.

Assuming a perfectly elastic collision, the ball (which was stationary with respect to the starting frame, and is now travelling at $-v$ relative to the rocket) will now be travelling at $+v$ relative to the rocket or $+2v$ relative to the starting frame.

The ball will continue travelling forward at $2v$, and the rocket will continue accelerating towards it. By the time it catches the ball again, it works out the rocket is travelling $3v$ (this can be seen either by symmetry arguments or explicitly working out the equations of motion). Relative to the rocket the picture is identical to the first bounce: the ball is at $-v$ and will bounce to $+v$ again.

Following it through in this way, we find that the behaviour of the ball relative to the (accelerating) frame of the rocket really is the same as if the ball was in a gravitational field.