Let's modify a bit this question so that we use a single reference frame
Let's imagine a laser shining light on an object. Let's put the reference frame at the object. In one instance the laser doesnt move, in the other the laser moves towards the object. There is a temperature probe on the object. The object absobs all light from the laser and turns it into heat. -When the laser moves towards the object will the object heat up faster due to the doppler shift ? Why ?
Consider this experiment:
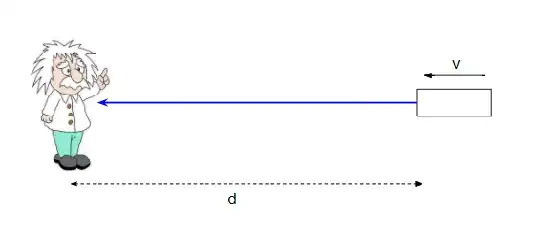
We have some laser with a power $P$, so if we run it for a time $t$ it emits an energy $E = Pt$.
Now suppose the laser is moving towards us at a speed $v$, and it starts a distance $d$ away. That means the time it takes to reach us is:
$$ t = \frac{d}{v} $$
So the energy it emits in that time is:
$$ E = P\frac{d}{v} $$
But at the beginning of the experiment there is already light in transit between the laser and us. The time the laser light takes to cross the initial gap $d$ is:
$$ t' = \frac{d}{c} $$
so the energy in transit is:
$$ E' = P\frac{d}{c} $$
That means the total energy that we receive in the time the laser takes to reach us is not just $E$ but:
$$ E_\text{total} = E + E' = Pd\left(\frac{1}{v} + \frac{1}{c}\right) $$
That's why we heat up faster when the laser is moving towards us.
Let's take this a step farther. The ratio of the energy we receive when the laser is moving to the energy we receive when it's stationary is:
$$\begin{align} \frac{E_\text{total}}{E} &= \frac{1/v + 1/c}{1/v} \\ &= 1 + \frac{v}{c} \end{align}$$
So using $E=h\nu$ we get:
$$ \frac{\nu'}{\nu} = 1 = \frac{v}{c} $$
and that is just the equation for the (non-relativistic) blue shift.
