I am attempting to make a rough estimate of the counts seen on a CCD spectrometer assuming I know the spectral radiance of a calibration source. I understand that this is not the same thing as radiometrically calibrating, but I want to make a calculation of the incident light and just come up with a rough estimate of how many photons strike a detector pixel. I know the quantum efficiency, the gain, and the diffraction efficiency, and I have dimensions for the pixel size if that is useful.
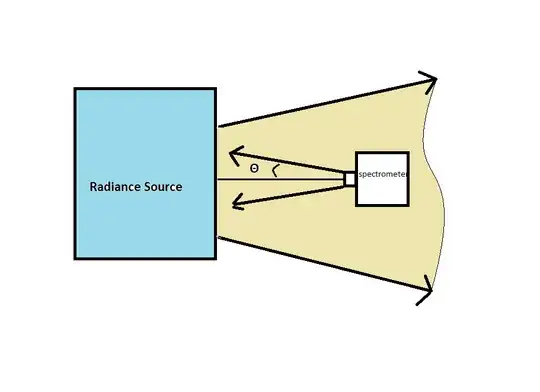
For my experimental setup, there is:
the calibration source, and integrating sphere that emits light through an aperture. I know the dimensions of this.
The spectrometer, with known slight size and field of view, apparent quantum efficiency at all wavelengths, as well as diffraction grating efficiency values. There is no lens or fiber optics cable in my setup.
A fixed distance between the spectrometer and radiance source, and I am making the assumption that the optical axes are aligned, and that the field of view of the spectrometer is completely encapsulated by the radiance source.
FIRST - How can I make an estimate of the power incident on the spectrometer slit?
I have some curve that provides radiance as a function of wavelength. It looks like this: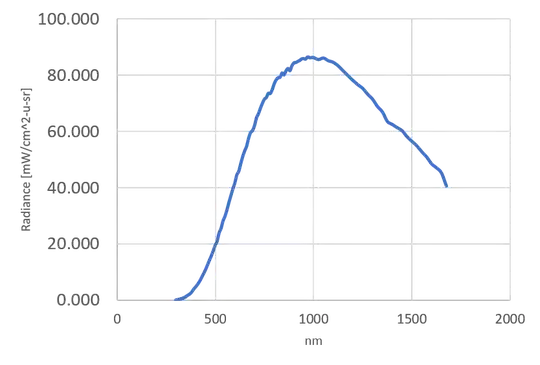
Knowing the area of the slit, and the f/# or NA, I should be able to calculate the throughput (etendue ) of the spectrometer, correct? If T is throughput:
$$ T = FA_{slit}\\ T = 2\pi(1-\cos(\theta))wl\\ $$
Where $\theta$ is the half angle of the slit field of view and $w$ and $l$ are the width and height of the spectrometer slit. If I multiply the radiance $L$ at some wavelength by this throughput, is that the power incident on the lens at a particular wavelength, or am I missing some geometric factor from the source? The units appear to work, so I am confused, $$P = [W/\mu] = TL = [m^2 sr][W/m^2\mu sr]$$. I believe this calculation assumes that the source is an 'extended' source.
From here, I would apply instrument efficiency values (loss due to diffraction, mirror reflectance, quantum efficiency) and integrate the radiance over the width of a pixel (in wavelength units). This would give me the final power incident on the pixel which can be converted to an incident photon rate at a specific wavelength. Finally, applying the Gain of the A/D converter and multiplying by some integration time should yield a rough estimate of the number of photons recorded.
SECOND - Knowing the instrument has some spectral resolution, but the pixels have some wavelength width, what is the best metric to integrate the radiance value over?
Any suggestions or references you may be able to provide are greatly appreciated, thank you.