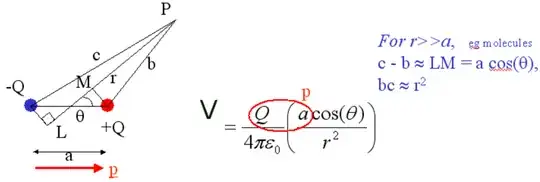I've been given the following graphic to help wrap my head around this.
If the potential can be shown to represent a $1/r^2$ relation, then I'm more than happy to accept that the electric field is hence a $1/r^3$ relation, but I need to accept the first part first:
Since $V = \frac{kQ}{r}$, this basically implies that $$r = \frac{bc}{c-b}$$ given the geometry of this graphic, yet I simply do not see it.
The important physical interpretation that you need to keep in mind is that the charges are opposite, so the $1/r$ pieces of their potentials cancel out. We'll see this happen explicitly in the math in the correct derivation.
But it also explains why your logic isn't quite enough to understand what's going on: You really do need those two opposite charges to cancel out the $1/r$ pieces. So you shouldn't start from just $V = kQ/r$ and then find the approximation for $r$ by plugging in the correct answer that you don't yet understand. That's not a helpful way of going about it. Instead, you should do the full derivation yourself.
First of all, I hope you can see from the geometry that \begin{equation} r \approx b + \frac{LM}{2} \approx c - \frac{LM}{2}. \end{equation} The reason is that as you take $P$ very far away, those lines $c$, $b$, and $r$ all become basically parallel, and they squeeze down onto each other. So $c$, $b$, and $r$ just represent different points along (roughly) the same line.
Now, accepting the equation above, you can immediately see that $LM \approx c-b$. You can also see that \begin{align} r^2 &\approx \left(b + \frac{LM}{2}\right)\left(c -\frac{LM}{2} \right) \\ &\approx bc + (c-b)\frac{LM}{2} - \frac{LM^2}{4} \\ &\approx bc + LM\frac{LM}{2} - \frac{LM^2}{4} \\ &\approx bc + \frac{LM^2}{4} \end{align} But when $r \gg a$ (and because $a \geq LM$), we know that $LM^2/4$ must have a small effect on the result, so we can just ignore it: $r^2 \approx bc$. That explains the two approximations shown in your figure. But I argue that's not enough to actually understand the total potential.
So onto the real derivation. You'll agree that (without any approximation) the full expression for the potential is \begin{align} V &= \frac{kQ} {b} - \frac{kQ} {c}. \end{align} Note that crucial minus sign! Next, we can start inserting our approximations: \begin{align} V &\approx \frac{kQ} {r-LM/2} - \frac{kQ} {r+LM/2} \\ &\approx \frac{kQ} {r-\frac{a\cos\theta}{2}} - \frac{kQ} {r+\frac{a\cos\theta}{2}} \\ &\approx \frac{kQ} {r} \frac{1}{1-\frac{a\cos\theta}{2r}} - \frac{kQ} {r} \frac{1}{1+\frac{a\cos\theta}{2r}} \end{align} In that last line, I haven't done anything fancy; I've simply pulled out the denominator. But now, that lets us use the approximation $\frac{1}{1 \pm x} \approx 1 \mp x$ for small $x$. In this case $x$ is $a\cos\theta / 2r$, and since $r \gg a$ this is small, so we can use that approximation: \begin{align} V &\approx \frac{kQ} {r} \left(1+\frac{a\cos\theta}{2r}\right) - \frac{kQ} {r} \left(1-\frac{a \cos\theta}{2r}\right) \\ &\approx \frac{kQ} {r} \frac{a\cos\theta}{r} \\ &\approx \frac{kQa\cos\theta} {r^2}. \end{align}
The key point is that $r$ (the distance to the center of the dipole) is not the same thing as the distances $b$ and $c$ from your test charge to the positive and negative charges of the dipole.
If the dipole separation isn't very large, then that isn't a big deal, as $1/r$ and $1/b$ will generally be quite similar, but they will have slight differences, and those are easy to calculate as a power series in $a$ when that is small: $$ \frac{1}{b} = \frac1r + \frac{a\cos(\theta)}{2r^2}+ O\left(\frac{a^2}{r^3}\right) \approx \frac1r + \frac{a\cos(\theta)}{2r^2}. $$
Now, here is the other important bit: because the charges are equal but opposite, the leading term in this series ($1/r)$ will be the same, so it will cancel out, but the corrections go in opposite directions, so that when you subtract the two potentials, the corrections add constructively: \begin{align} \frac{1}{b} &\approx \frac1r + \frac{a\cos(\theta)}{2r^2} \\ \frac{1}{c} &\approx \frac1r - \frac{a\cos(\theta)}{2r^2} \\ \implies \frac{1}{b} - \frac{1}{c} &\approx \frac{a\cos(\theta)}{r^2}. \\ \end{align} This is where the $\propto 1/r^2$ potential comes from - as a leading-order correction to the two distances, and it is most cleanly obtained through the Taylor series of $1/b$ when it is displaced.
That means that, if you insist on seeing things on the specific geometry of your diagram, then the geometry is only exact in the limit where $r\gg a$, i.e. when the lines $(-Q)P$, $LM$ and $(+Q)P$ are parallel; if they're not parallel, then the identity $c-b=LM$ is false. That means that the geometric identity you've written down, $$ r= \frac{bc}{c-b}, $$ can never be right, because it makes no reference to $a$. If you want to build a version of that identity which does hold, then your best bet is to work from the cosine law of both triangles, \begin{align} b^2 & = r^2 + \frac{1}{4}a^2 - ra\cos(\theta),\\ c^2 & = r^2 + \frac{1}{4}a^2 + ra\cos(\theta). \end{align} Thus:
If what you want is the potential, then the thing to do is to re-phrase these as $$ \frac{1}{b} = \frac{1}{r}\frac{1}{\sqrt{1-\frac ar\cos(\theta) + \frac{a^2}{r^2}}}, $$ and expand the square root using Newton's binomial series.
If what you want is the length difference $c-b$, then that's best done via $$ b-c = r\left[\sqrt{1+\frac ar\cos(\theta) + \frac{a^2}{r^2}} - \sqrt{1-\frac ar\cos(\theta) + \frac{a^2}{r^2}}\right] $$ and again expanding using the binomial series.
If what you want is a correct version of $r=bc/(c-b)$, then you can put in those expressions to get $$ \frac{bc}{c-b} \approx \frac{r^2}{a\cos(\theta)}, $$ and since you're looking at the $r\gg a$ limit, that tells you just how wrong the $r=bc/(c-b)$ identification is in this geometry.
