Which interaction is responsible for secondary electron emission?

Question

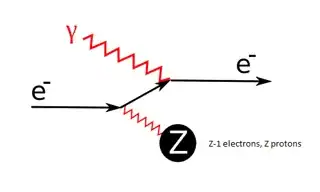
When imaging with SEM (Scanning Electron Microscopy) an incident electron ejects an electron from the surface of the sample, which is then detected in order to create an image. In that case I guess that the process is dominantly electromagnetic (right?), so can I write such an equation to describe the process:

$$e^- + X \overset{\gamma*}{\rightarrow} e^- + X^+ + e^-$$

where $\gamma*$ describes a virtual photon, $X$ the target atom and $X^+$ the target atom ionized after the interaction?

My real question is actually about an ion (say $He^+$) hitting a target atom and sputtering a secondary electron. Is it still the electron of the $He^+$ interacting electromagnetically with the target electron, or something else that I cannot think of? And if yes, can I then describe the process as follows:

$$He^++X \overset{\gamma*}{\rightarrow} He^+ + X^+ + e^-$$

? Would there be a chance that the incident ion loses its electron, like:

$$He^+ + X \overset{\gamma*}{\rightarrow} He^{++} + X^+ + 2e^-$$

?

Thanks a lot in advance for your answers.

Answer 1

One has to give boundary conditions,energy and momentum of beam. For low energies the behavior can be well modeled , even though the underlying interaction is quantum mechanical and for accuracy, it will always be described by virtual photon exchanges.

Look at the photoelectric effect, a real photon hits a neutral atom

The black electron line represents the "orbital" of the electron before interacting with the incoming photon. If the photon frequency is higher than the binding energy of the electron, it will ionize the Z nucleus.

In the case of surfaces there will be a collective diagram between conduction band electrons, the ones with the weakest binding energy to the lattice, which will be kicked out if the conduction band binding energy is supplied by the photon.

The diagram can be extended to a virtual photon exchange between the He+ and the last electron of the nucleus, or the conduction band of a surface.

This is simple for single nuclei. For nuclei in a lattice the specific interactions will depend on the way electrons are distributed , in bands, the conduction band being the less bound state. Again a specific model has to be invoked, but the classical models in the first link are adequate to describe the statistical behavior of the scattering.