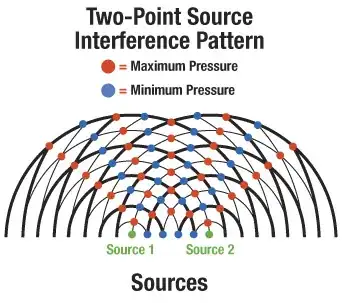
I read that two incoherent sounds add up $+3db$, and two coherent $+6db$. Tell me how does this not break law of conservation of energy.
$+3 db =$ double power
$+6 db =$ quadruple power
If we have one sound source that creates 1 Watt sound power,and add another 1 Watt sound source,we have total of 2 Watts of sound power,it does not matter if the sounds emitted are coherent,thats absolute maximum limit before breaking law of conservation of energy.
Please note,two speakers using pistonic motion of fixed size surface ( all normal speakers ) to create sound do add up +6db if they are closer together than 1/2 of wavelenght,that is becose the effective radiation surface doubles,so efficieny doubles,there is effect called mutual coupling.
Two times efficiency + two times power does indeed result in +6db,but as far as I am aware,this doesnt work when sound sources are more than 1 wavelenght away and nowhere did it mentioned that coherent sounds add up +6db only when sound sources are close together,it seemed to be written as if its universal law that exist no matter the position of sound source.