Why does a leaning bike not fall over?

Question

This question has been bothering me for a while now. Everywhere I look, everyone talks about 'fictitious forces' and how they apparently explain the bike being in equilibrium. However, if we just look at a simple force diagram, we can see that turning moments around certain points are unbalanced: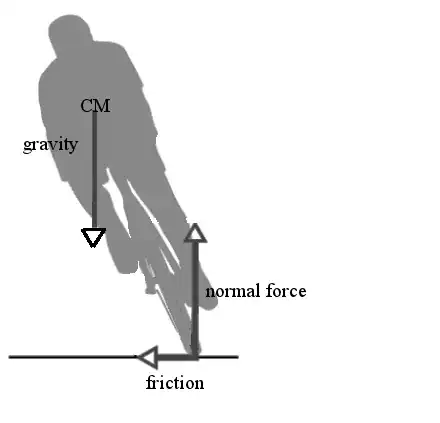

If we take moments around, for example, the point where the wheel touches the ground, we obtain that a resultant moment of $amg\cos \theta$, where $a$ is some length, $m$ the mass of the combined system of the driver and the bike, and $\theta$ the angle between the bike and the ground, is acting so as to make the system fall down in the direction of the centre.

This moment will always be 'towards the centre' - irrespective of the bike's position. That means it should fall down. So why doesn't it? Clearly, either there should be no resultant moment, or the resultant moment throughout the duration of one lap made by the bike should be $0$, but none is evidently the case here. What am I missing?

Answer 1

In the inertial frame, the torques are unbalanced and the rider's rotational momentum about a point on the ground changes. It's just that this change does not result in the rider toppling.

If instead you consider the frame where the rider is at rest, then this (accelerating) frame will have fictitious forces opposite the acceleration appear.

These forces will act through the center of mass of the rider, and will be in the opposite direction of the acceleration. Since the rider is accelerating to the left, there should be a fictitious frame force to the right. This balances the torques about the tire contact.

Answer 2

The reason that the biker doesn't fall when leaning in a curve is the centrifugal force on the CM of the biker. You see this best when the biker moves in a circle in a curve. The torque by the gravitational force is exactly balanced by the torque due to the centrifugal force on the biker. A description you will find here.

Quantitative description: As you seem not to accept that the centrifugal force explains the problem, I give you a quantitative derivation. The torque $T_g$ of gravitational force on the center of mass relative to the intersection of axis driver/bike with the ground is $$T_g=mgacos\theta$$ where $a$ is the distance of the center of mass from the intersection of the axis with the ground. The opposing torque of the centrifugal force on the center of mass with respect the same point on the ground in the frame rotating with the biker is $$T_{cf}=\frac{amv^2 sin \theta}{r}$$ where $v$ is the velocity of the bikers center of mass and $r$ is the (local) radius of the bikers center of mass path. Thus you have a resultant torque zero for $$T_g=mgacos\theta=\frac{amv^2 sin \theta}{r}=T_{cf}$$ From which follows the inclination of the axis of the biker in equilibrium $$tan \theta=\frac {g r}{v^2}$$ This shows that the resulting torque acting on the biker is indeed zero for a certain angle of inclination, which confirms the experience of all bikers driving in a curve.

Answer 3

Indeed if the bike was travelling in a straight line, the bike would fall over. It is the circular motion that has the rider falling towards the centre of the circle, but the constant change in direction prevents the bike from simply falling to the ground.

Think of a velodrome where bike speed races are held. When the rider is moving along the banked curve, what would happen if the curve became straight but still banked? Well the rider would begin to drop down the bank, not because he is forcing the bike there, but because this would naturally occur. His bike would be falling over due to the imbalance of the moments you mention.

Answer 4

Simply because in doing the calculations in the frame of reference of the bike itself, you are doing these calculations in an accelerated frame of reference, and you need to factor in the acceleration to balance everything.

If you did the calculations in an inertial frame of reference, then, in that frame, the moment does exist, but it is balanced by the moment created by the lateral acceleration through the center of mas to the outside of the turn.