I have a doubt in understanding the concept of internal energy. The internal energy of a system is equal to U=f/2nrT, where T is the temperature. Now, also we know that dU=Q-W Then if heat is zero, magnitude of work done should be equal to that of internal energy. But we see that, W=nRdT Using it both, we get: f/2nRdT=nRdt Now,that's what confuses me. Can anyone clarify where my concept lack?
Asked
Active
Viewed 6,483 times
2 Answers
1
If heat exchange is zero then the process will be adiabatic and in that case the work done by the gas will NOT be equal to
nR(dT)
rather it will be equal to the expression given in the image. if you use the expression given in the image then you get the answer. I am also posting the proof calculation of work done in adiabatic process.
So that is where the problem is lying in your solution.
Devansh Mittal
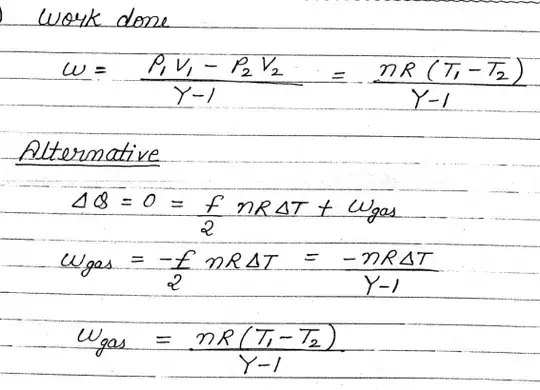
- 2,577
0
First of all, if we have an ideal gas then $pV=nRT$, so $p=(nRT)/V$. Then, $W = (nRT)/V dV$. Your Work equation is wrong.
To clarify on how to develop from $dU=dW$ in an alternative way, we can obtain some interesting properties.
We have $dU = dW \rightarrow U = W$ , for an adiabatic process. (It is also known that $C_p=(f/2)nR+nR$ and $C_v=(f/2)nR$ ; Heat capacities for constant pressure and volume, respectively)
So:
$dU = (f/2)nRdT = (C_v)dT , as C_v=(f/2)nR$
Now we can develop the equation:
$(C_v)dT = -((nRT)/V)dV <-> $
$(C_v)dT/T = - ((C_p-C_v)/V)dV$
Integrating both terms, (assuming $T_0$,$V_0$ as initial $T$ and $V$, respectively)
$C_v*ln(T/T_0) = -(C_p-C_v)*ln(V/V_0) <->$
$ln((T/T_0)^{C_v}) = ln((V/V_0)(C_v-C_p)) <->$
$T/T_0 = (V/V_0)^{((C_v-C_p)/C_v)}$
And as $\gamma=(C_v/C_p)$: $T/T_0 = (V/V_0)^{(1-\gamma)}$ ; where $\gamma$ is a greek letter, which represents the adiabatic constant.
We can say that, $TV^{(\gamma-1)} = T_0 V_0 = constant$ We can also obtain $PV^{\gamma}$ = constant applying the Ideal gas law in $TV^{(\gamma-1)} = constant$.
