Short answer: the smooth upwards-decreasing thickness profile turns into a constant function when the minimum, stable thickness for the film is reached.
This transition point moves downward with time:
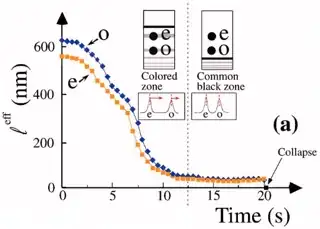
Source: Ropars et al., Dynamics of gravity-induced gradients in soap film thicknesses (e-print).
Long answer:
Soap film interference
The thin film of soap solution offers two surfaces of reflection: the frontal one, a transition from air to film, and the back one, from film to air. The bands are caused by the interference between the reflections at the two interfaces, their color reflecting the difference in optical path length, which in turn depends on the film thickness ($d$ in the scheme below).
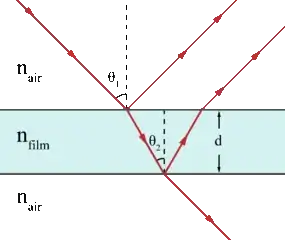
The reflection at a "hard interface" (from a region with lower refraction index such as air to one of a higher refraction index such as soap film) leads to an inversion in the wave phase (a change in $\pi=180^{\circ}$), while a reflection at a "soft interface" (from higher to lower refraction indexes) leads to no change in phase. That means that if the film is too thin relative to the wavelength, then destructive interference will prevent the light from being reflected: that's the dark band on the top, which is the thinest portion of the film (between about $10$ nm or $25$ nm and $50$ nm), do to the effect of gravity.
The color of the soap film under white light, as a function of thickness is shown in this figure:
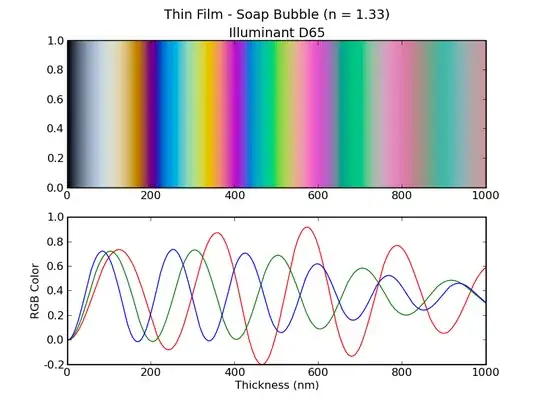 Source.
Source.
The question is about why the transition from bright to dark is abrupt. So first it's relevant to point out that it doesn't have to be abrupt, but can be smoother for an away-from-equilibrium film:
 Source.
Source.
Abrupt transition
As for the abrupt transition, it's located at the transition line between the non-stationary$^1$ region where the solution is still flowing down and the stationary region where gravity is counterbalanced by, e.g., capillary forces (the capillary length for the film is about $4$ meters) and the Marangoni effect. The films walls are kept apart by repulsion forces, which are mainly (Wikipedia, and also this answer): "steric (the surfactants can not interlace) and electrostatic (if surfactants are charged)".
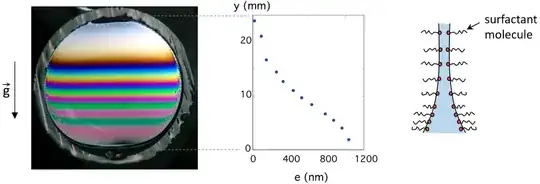 Source: Gaulon et al., Sound and vision: visualization of music with a soap film.
Source: Gaulon et al., Sound and vision: visualization of music with a soap film.
$^1$: I'm using stationary instead of equilibrium, because besides Marangoni flows, the stable state may include dynamic phenomena such as marginal regeneration, which consists in convection flows along the frame of the soap film (see, e.g., this paper, e-print) which seems necessary to prevent rupture, according to this paper (this need could conceivably explain the relatively short life time of films on square frames (e-print).





