What will be the nature of the motion of a simple pendulum for larger angular displacement? Will that be a periodic motion? If so, will the time period increase or decrease?
Asked
Active
Viewed 1,632 times
1 Answers
0
A pendulum in general is described by the equation of motion: $$\ddot\theta = -\frac{g}{L}\sin(\theta)$$ We normally approximate the problem with the approximation theta $\sin(\theta)\approx \theta$ which is a Taylor approximation. We could do a higher order Approximation,$\sin(\theta)=\theta-\frac{1}{6}\theta^3$, but this would make the differential equation hard to solve by hand. What this would do is add an term to the time it would take to compelte period, thus making it take longer for the pendulum to swing at larger displacement. However this term is smaller than the first term. The period will then become something like this: $$ T = 2\pi\sqrt{\frac{l}{g}}(1+\frac{1}{16}\theta_0^2)$$
So yes this motion will be periodic and the time it takes will be slightly longer, becoming more accurate the higher order approximation you do.
But practically, below you find a figure of the deviation from the true period of the small angle approximation as a function of the angle.
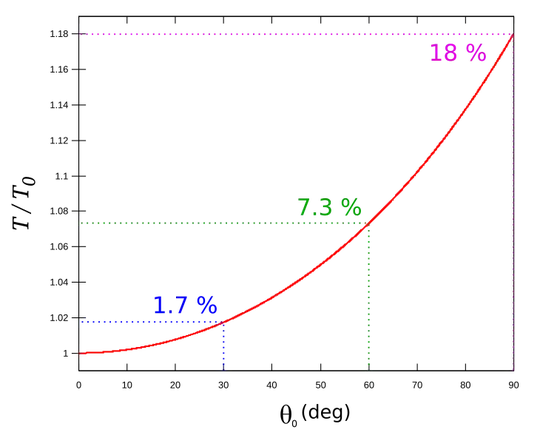If you want to get into the mathematics of this I would suggest you read this
Gijsv
- 52