2

Situation: (self-made)

A (green) block is partially immersed in a (blue) liquid and the vessel is accelerating upwards with an acceleration $a$. The block is observed by (stick-figure) observers $O_1$ and $O_2$, one at rest and the other accelerating at acceleration $a$ upward as shown in the figure. What is the total buoyant force on the block as observed by $O_1$ and $O_2$?

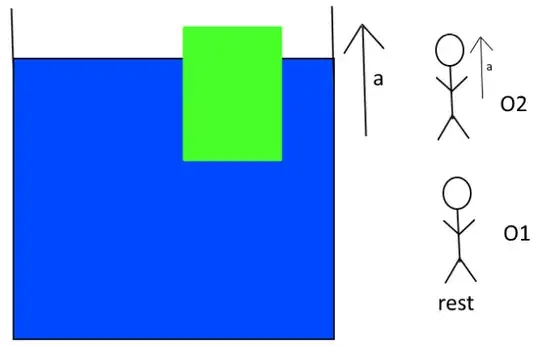enter image description here Picture courtesy: Me+Paint.NET

I believed that the buoyant force on the object should've been different for both the observers. I have detailed my thought process below.

For $O_1$: Since $O_1$ is at rest, we can consider it as ground frame. I found that what I had thought was correct, that the buoyant force is $=V_{block}\cdot\rho_{block}\cdot g_{eff}$ for $g_{eff}=g+a$.

For $O_2$: Since $O_2$ is accelerating at $a$ along with the vessel, so with respect to $O_2$, vessel is at rest. Hence, buoyant force (in the frame of $O_2$) = weight of block (for vertical equilibrium) = $V_{block}\cdot\rho_{block}\cdot g$.

But, the answer I gave is not the correct answer. The correct answer is that the buoyant force is same for both observers. Thus, I need help understanding:

Why is the buoyant force on the object same even for the two different observers?

Wolgwang
  • 127
  • 2
  • 14
Gaurang Tandon
  • 841

1 Answers1

3

In the reference frame of $O_1$, gravity has the value of $g$. $O_2$ is accelerating upward, so feels heavier: for her $g_{eff} = g + a$. (Here I'm using $g_{eff}$ to represent the apparent gravitational field in $O_2$'s reference frame). In the hydrostatic case, the buoyant force depends on the submerged volume of the block, the density of the liquid, and the effective gravity. So according to $O_2$, the buoyant force on the block is $\rho_l * (g + a) * V_{submerged}$ [it is also, as you say, equal to the weight of the block, which is $m_{block} * (g + a)$]. Naively the buoyancy force according to $O_1$ would be $\rho_l * g * V_{submerged}$. But this is wrong.

The liquid is at rest according to $O_2$. To $O_1$ it is is accelerating upward. In an accelerating liquid, the hydrostatic approximation (that is, the relationship $p = \rho_l g h$) is not valid. For example, normally, if you release a buoy at the bottom of a bucket of water, it floats to the top. But if at the same time, you drop the bucket off a cliff, the buoy does not rise, but remains at the bottom of the bucket. Because the liquid is accelerating downward at $g$, it is essentially weightless, and produces no buoyancy force. $O_1$ experiences gravity of $g$, but sees the liquid accelerating upward at $a$, and so concludes that the buoyancy force is $\rho_l * (g + a) * V$, exactly the same as $O_2$. In retrospect, it is clear that both observers must report the same buoyancy force, because what it actually is is an integral of the pressure over the surface of the block, which should appear identical to both. For $O_1$, this buoyancy force is greater than the gravitational force ($m_{block} * g$), and the block accelerates upward. For $O_2$, the two forces are equal (effective gravity being greater for $O_2$) and the block does not accelerate.

Ben51
  • 10,037