1

Suppose we have a mass $m$ dangling from the ceiling on a vertical rope of length $\ell$ with uniform mass density $\lambda$ per unit length. The weight of the mass $mg$ is balanced exactly by the tension in the rope.

Now, suppose the rope is cut at the top of the ceiling. After a moment, the tension in the rope will be (pretty much) zero throughout and the mass will be in free fall. But, presumably the process is actually continuous, and over some period of time the tension in the rope will decrease from its initial value $T(y)$ (depending on the distance $y$ from the ceiling). How does $T(y)$ evolve over time?

Qmechanic
  • 220,844
Sameer Kailasa
  • 235

4 Answers4

3

But, presumably the process is actually continuous, and over some period of time the tension in the rope will decrease from its initial value $T(y)$ (depending on the distance $y$ from the ceiling). How does $T(y)$ evolve over time?

A single value changing over time won't be a useful model. In a static or slowly evolving situation, we can model the string as massless and perfectly rigid. In this case, a single value for $T$ throughout the item is reasonable. If you continue to use this ideal model when the rope is cut, then we would consider the tension goes to zero immediately.

But if this model is insufficient, then assuming it has a single $T$ throughout is also insufficient. Instead, changes in the forces on the rope propagate from one part of the string to another at a finite speed (often very close to the speed of sound in the material). In your example, if the rope is light, then immediately after the cut, regions of the rope near the cut will have a tension near zero, while regions far from the cut will have a tension equal to $T$. Rather than a single value in the material smoothly changing over time, different portions will differ dramatically.

A sensor connected to the rope at the other end would see the force from the rope drop rapidly to zero, just later than when it was cut. The lighter the rope, the more rapid the drop.

BowlOfRed
  • 42,997
  • 3
  • 68
  • 123
2

Let's suppose for simplicity that the cut happens instantaneously and that the rope remains straight after it is cut.

The magnitude of the tension felt by the mass is initially $mg$, since it has to balance the force due to gravity. If the rope is cut at time $0$, the information that the rupture has happened will start to travel towards the mass at velocity $v_s$, where $v_s$ is the speed of sound (longitudinal wave) in the material the rope is made of, and will reach the mass at time $t(y)=y/v_s$, where $y$ is the distance from the cut.

As a reference, the speed of a sound in nylon is $1070$ m/s according to this page. Therefore if $y=1$ m the mass will "notice" that the rupture has happened at time

$$t(1 \text{m}) = \frac{1}{1070} \text{s} \approx 10^{-3} s$$

So, from the point of view of a human, the rupture will happen almost immediately.

In this ideal case, the tension will drop instantaneously from $mg$ to $0$ at time $t(y)$. In a real case, however, the drop will happen in a finite time.

Take also a look at this plot of tension vs time during the rupture of a climbing rope, taken from this document from UIAA:

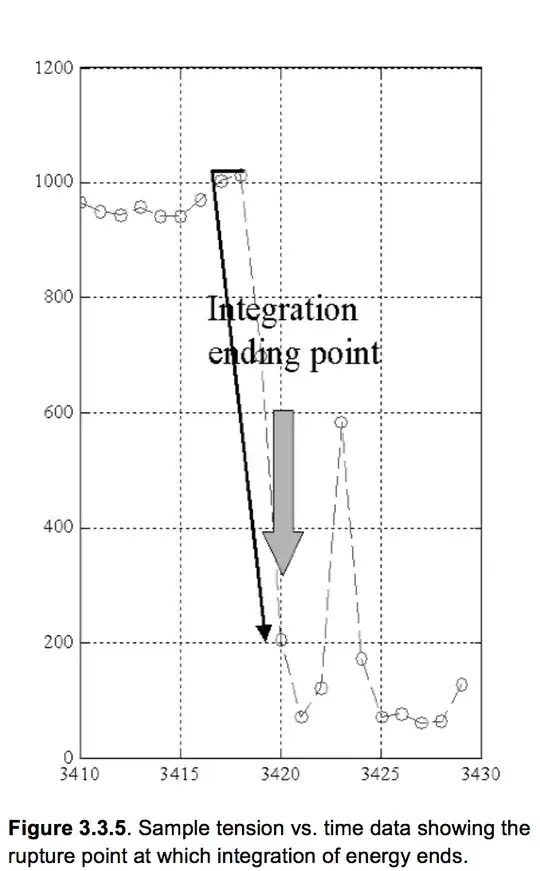
enter image description here

(On the $y$ axis the unit is $10 \cdot$ N, don't know about the horizontal axis but I'm guessing $10^{-3}$ s...these people should really learn to label their axes though!)

valerio
  • 16,751
1

Consider a mass is attached to a vertical spring, dangling from the ceiling. If you suddenly detach the spring from the ceiling, the spring starts oscillating close to SH

Now, in the case of rope, because of presence of some elasticity of the rope, similar motion may be seen. Unlike spring, near SHM motion drys out very fast and practically, you don't see any motion.

Vikash Kumar
  • 510
0

It would be very very hard to calculate this function.

Suppose that you're cutting the rope with a scissor and during that time, the rope will look like this:

enter image description here

Points $A$ and $B$ will have different mass densities per unit length as $B$ would be more stretched than $A$. This implies that each vertical section of the rope will have a different mass density and obviously, a different tension which would altogether make it more harder to calculate that function.

Aaryan Dewan
  • 1,820