Calculate velocity when mass hit the Sun

Question

Suppose no planet exist in the solar system, only the sun.

Then place a mass at a distance $r$ from the sun.

At what velocity does the mass 'hit' the sun?

Suppose both mass and sun are points in space and movements happen in a line. I know the relativistic consequences of this, just simplify things a bit...

My question rises from calculating the integral $v = a(t)dt$.

I know the acceleration by Newton's law, given by $G\frac{M}{r^2}$, but it depend on the distance and I'm not integrating over distance, but over time.

In the end, $G*M$ are constant, hence I am getting integral of $\frac{1}{r^2} dt$, and I'm stuck.

I'm not looking for answers involving mechanical conservation of energy, simply answers involving this integration method.

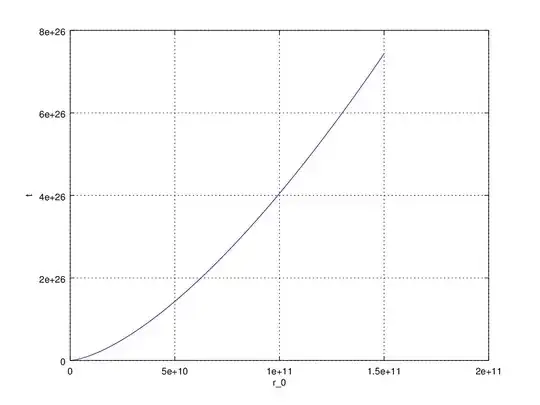
Also, how much time does this mass take to hit the sun?

I wrote out the integral of $\int G\frac{M}{r^2}t, dt$, but cannot go further with my actual knowledge.

Answer 1

So we can look at this in terms of differential equation: $$\frac{d^2r}{dt^2}=-\frac{G(M+m)}{r^2}$$where $M$ is the mass of the sun and $m$ is the mass of the object that is going into the sun. $($I have written it like this in case the mass of the object $m$ is large enough to create a noticeable acceleration of the sun$)$. Multiplying both sides by $dr$ we get: $$\int_{r_0}^r\frac{dv}{dt}dr=\int_{r_0}^r -\frac{G(M+m)}{r^2}dr$$ $$\int_0^v v\ dv=\int_{r_0}^r -\frac{G(M+m)}{r^2}dr$$ $$\frac{1}{2}v^2=\frac{G(M+m)}{r}-\frac{G(M+m)}{r_0}$$ $$v=\sqrt{\frac{2G(M+m)}{r}-\frac{2G(M+m)}{r_0}}$$ Where $r_0$ is the initial radius and $r$ is the final radius $($both measured from the centre of the sun$)$. Now getting onto your second question we should continue from where we left off with:$$v=\frac{dr}{dt}=\sqrt{\frac{2G(M+m)}{r}-\frac{2G(M+m)}{r_0}}$$ $$\frac{dr}{dt}=\sqrt{\frac{2G(M+m)r_0-2G(M+m)r}{rr_0}}$$ And rearranging for $dt$ we get: $$dt=\frac{\sqrt{rr_0}dr}{\sqrt{2G(M+m)r_0-2G(M+m)r}}$$ $$dt=\sqrt{\frac{r_0}{2G(M+m)}}\sqrt{\frac{r}{r_0-r}}dr$$ Substituting in for $$u=\sqrt{\frac{r}{r_0-r}}$$ and rearranging we get $$dr=\frac{2r_0u}{(1+u^2)^2}du$$ and so $$dt=\sqrt{\frac{r_0}{2G(M+m)}}\frac{2r_0u^2}{(1+u^2)^2}du$$ Now, as $r\to r_0,\ u\to\infty$ and as $r\to r_f,\ u\to u_f$ where $r_f$ is the radius of the sun and $$u_f=\sqrt{\frac{r_f}{r_0-r_f}}$$ $$dt=\frac{2r_0^{3/2}}{\sqrt{2G(M+m)}}\int_{u_f}^{\infty}\frac{u^2}{(1+u^2)^2}du$$Solving this for $t$ gets us: $$t=\frac{2r_0^{3/2}}{\sqrt{G(M+m)}}\bigg(\frac{\pi}{2}-\bigg(\tan^{-1}(u_f)-\frac{u_f}{1+u_f^2}\bigg)\bigg)$$

Hope this helps :). If you need me to expand on any points I can just leave a comment.

Answer 2

I tried to do a quick code of the above equations and got this graph of t and r_0. Setting the r_0 as the sun earth distance. And the masses of that of the sun and the earth. The peak reaches around 7^26 seconds which is about 2 months. Also feel free to correct me if im wrong!