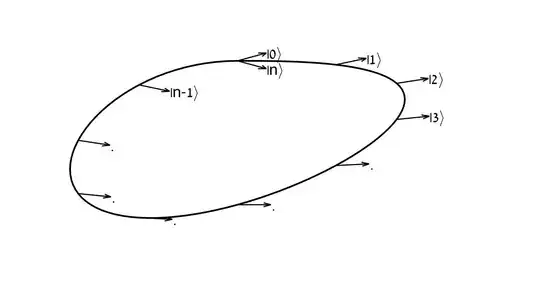
The following figure depicts a closed path in the parameter space and shows the variation of the state's normalized eigenvectors in $n$ discrete point along the path. The last point of the path $n$ coincides with the first point $0$.
 The Berry phase is the total of the accumulated phases along the path:
$$ \phi = \lim_{n \to \infty}\arg(\langle 0|1 \rangle\langle 1 |2 \rangle .,.,.,\langle n-1 | n\rangle\langle n | 0\rangle)$$
This definition makes sense, since it is gauge invariant and a local phase transformation on every point of the path
$$|k' \rangle = e^{i \alpha_k}|k \rangle$$
does not change its value because:
$$\langle l' |k' \rangle = e^{i \alpha_k - i\alpha_l}\langle l' |k' \rangle$$
We can choose a gauge transformations such that:
$$|0' \rangle = |0 \rangle$$
(Initial condition), and
$$\arg(\langle k' |k' +1\rangle) = 0 $$
The second condition makes the direction of the eigenvector at the $k+1$ -th point parallel to that of the $k$ -th point. Thus in the basis $|k' \rangle$, the vectors are parallel transformed.
The Berry phase is the total of the accumulated phases along the path:
$$ \phi = \lim_{n \to \infty}\arg(\langle 0|1 \rangle\langle 1 |2 \rangle .,.,.,\langle n-1 | n\rangle\langle n | 0\rangle)$$
This definition makes sense, since it is gauge invariant and a local phase transformation on every point of the path
$$|k' \rangle = e^{i \alpha_k}|k \rangle$$
does not change its value because:
$$\langle l' |k' \rangle = e^{i \alpha_k - i\alpha_l}\langle l' |k' \rangle$$
We can choose a gauge transformations such that:
$$|0' \rangle = |0 \rangle$$
(Initial condition), and
$$\arg(\langle k' |k' +1\rangle) = 0 $$
The second condition makes the direction of the eigenvector at the $k+1$ -th point parallel to that of the $k$ -th point. Thus in the basis $|k' \rangle$, the vectors are parallel transformed.
Please notice that the last term in the Berry phase $\langle n | 0\rangle$ cannot be rotated to zero, because the phase of $|0'\rangle$ is fixed by the initial condition and the phase of $|n'\rangle$ is fixed by the condition $\arg(\langle n'-1 |n' \rangle)=0 $. Thus we are left with only one term in the Berry phase :
$$ \phi = \arg(\langle n' | 0'\rangle)$$
It must be emphasized that the above expression is valid only in the parallel transport gauge system $\{|k' \rangle\}_{k=0, ., ., ., n}$. The value of this phase is equal to the original value due to gauge invariance.
Going to the continuum, we have:
$$\arg(\langle k |k+1\rangle) \rightarrow \arg(\langle n(t) |n(t+\Delta t)\rangle) $$
Where in the continuum, we use the points $n$ in the parameter space to parametrize the eigenvectors; We have:
$$|n(t+\Delta t)\rangle = |n(t)+\frac{d n}{d t} \Delta t \rangle = |n(t)\rangle + \frac{\partial |n(t)\rangle}{\partial n^i}\frac{dR^i}{dt}\Delta t$$
Thus:
$$\arg(\langle n(t) |n(t+\Delta t)\rangle) =\mathrm{ Im}(\langle n(t) | \frac{\partial |n(t)\rangle}{\partial n^i})\frac{dn^i}{dt}\Delta t$$
(because the vector is normalized, we have $\arg(1+x) = \mathrm{Im}(x)$). The inner product $\langle n(t) | \frac{\partial |n(t)\rangle}{\partial n^i})$
is pure imaginary because:
$$\mathrm{ Re}(\langle n(t) | \frac{\partial |n(t)\rangle}{\partial n^i}) \rangle= \frac{1}{2} (\langle n(t) | \frac{\partial |n(t)\rangle}{\partial n^i}\rangle + \langle \frac{\partial |n(t)\rangle}{\partial n^i} | n(t)\rangle) = \frac{\partial }{2\partial n^i} \langle n(t)| n(t) \rangle = 0$$
(since $\langle n(t)| n(t) \rangle =1$).
Thus we may write the Berry phase as:
$$ \phi = \oint \langle n(t) | \frac{\partial |n(t)\rangle}{\partial n^i})\frac{dn^i}{dt}d t$$
The integrand in the last expression is the Berry connection.
