For plotting P-V diagrams, is it necessary for each step need to be reversible?

Question

While explaining cyclic process with the help of P-V diagrams, the teacher told us the difference between a cyclic process and a reversible process. He said that in cyclic process, the system goes back to its initial conditions, but may not retrace the path in the P-V diagram, while in case of a reversible process, it is of utmost necessity that the system retraces the graph to go back to the original conditions.

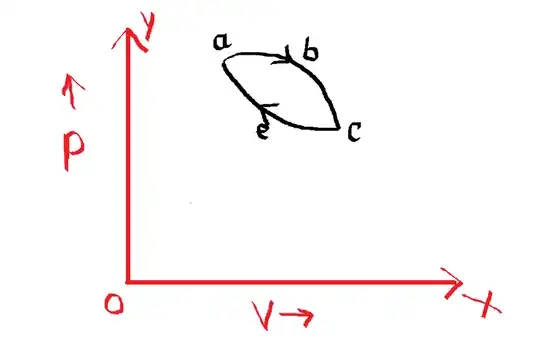
For example, this is a cyclic process but not a reversible process as it does not retrace the graph, or in other words, it does not keep the surroundings unchanged when it returns to the original conditions.

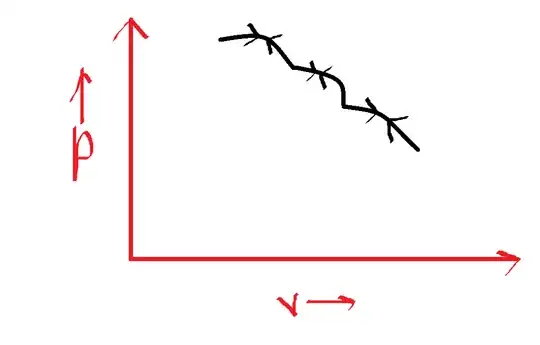
This is a reversible process, where the graph is retraced:

A classmate of mine started arguing with the teacher that in order to plot a graph of a thermodynamic process, each step of each of the processes constituting the total change, should be reversible, whether or not the process is as a whole reversible. As per him, if we consider this diagram:

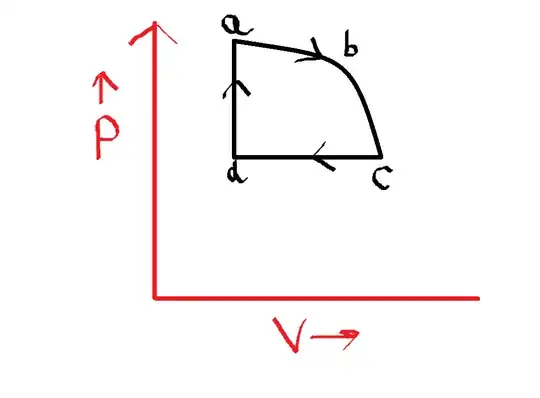
then the total process is not reversible but cyclic, but each of the steps (viz. $a$ to $b$, $b$ to $c$, $c$ to $d$, and $d$ to $a$) are reversible. As per him, it is an absolutely necessary condition that each step must be reversible so as to plot the graph, otherwise one shall not be able to measure the state functions.

The teacher said that he had never heard of something like this.

Can anyone explain who is right: the teacher or my classmate? It seems that my classmate is wrong, simply because if each step is reversible, then the whole process would become a reversible process. I haven't studied thermodynamics to a great depth, so I don't know who is correct.

Answer 1

Short answer: both are wrong.

Why is the teacher wrong? Because there can be reversible cyclic processes which does not retrace the graph (such as your Figure 2). For example, the Carnot cycle, which is reversible.

Why is the student wrong? Because a curve in the pV diagram does not imply that the process is a sequence of reversible steps. If other words it is possible to represent irreversible steps in the pV diagram. For example, consider an idealized thermal engine working between two sources and following the Diesel cycle. Although this cycle is well defined in the pV diagram, a heat engine operating between two sources and following it undergoes a cyclic irreversible process, since its efficiency is less than Carnot efficiency.

To avoid this sort of confusion we only need to stick with the definition of reversible processes, namely those which are quasi-static, have no friction and have no irreversible exchange of heat (exchange through finite temperature difference). If a process is quasi-static then we can draw a curve in the pV diagram, since it is a succession equilibrium states, which has definite values for thermodynamic variables. It may be reversible or irreversible though.

If you want to know whether a cyclic process is reversible or not it is not enough just looking at its curve. You must calculate, for example, the Clausius integral, $$\oint \frac{dQ}{T_F},$$ where $T_F$ is the temperature of the source. If this integral is zero, then the cycle is reversible and if it is negative (it cannot be positive) then the cycle is irreversible.