If torque has a different value depending on the set origin, how can rotational kinetic energy be absolute?

Question

I'm going to illustrate this confusion of mine in a thought experiment (poorly):

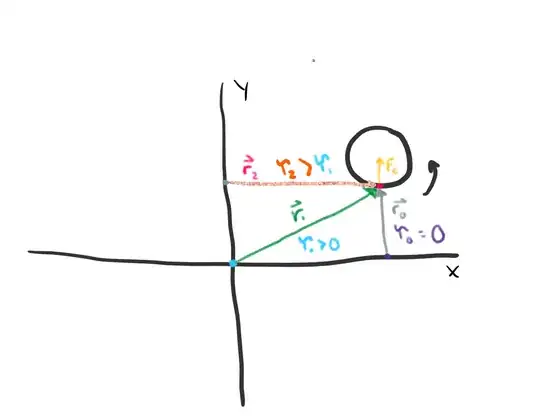
Here we have origins for $\vec r_2, \vec r_1,$ and $\vec r_0$.

What's undeniable is that this wheel is spinning in uniform circular motion on it, as I am defining it. There is no tangent acceleration on the particles on this wheel. Here we have $3$ different origins at different places, which have their own distance vectors $\vec r_0, \vec r_1, \vec r_2$ to that point. The particle is experiencing a centripetal force colored in yellow. From the origin as the center of mass of the wheel, the radius vector and the force vector would be anti-parallel and thus no torque would be active on the particle. However, according to these origins I've colored, there is a torque on the particle at each origin with the exception of $r_0$, although in the next instant of time there will be once the position vector changes as it follows the particle. This notion that it's feeling a torque with its only active force on that particle being the centripetal force bothers me. The particle on the wheel is not actually experiencing a torque! How could it? It doesn't actually, or at least relative to the center of the wheel, but it does relative to the radius vectors? I know torque is different relative to your origin, but how can we have this scenario I've underscored? It makes me feel like torque can give unreliable interpretations on the motion of this rotating particle.

And, in addition, like its linear analog, applying a torque on an object will give it energy, just like applying a force on an object will give it energy. But the torque here depends on the vantage point, so what it seems like to me is that the wheel is gaining different amounts of energy from different vantage points depending on the torque it's experiencing according to each radius vector (or vantage point/origin).

How do I make sense of all this? The kinetic energy on the wheel has to be uniform regardless of vantage point.

Answer 1

The answer is that rotational kinetic energy is not, in general, invariant under coordinate transforms. What is invariant is the rotational kinetic energy about the center of mass. To see why, look at the kinetic energy in polar coordinates: $$ K = \frac{1}{2} m \dot{r}_{\mathrm{CM}}^2 + \frac{1}{2} m r_{\mathrm{CM}}^2 \dot{\theta}_{\mathrm{CM}}^2 + \frac{1}{2} I_{0} \omega^2 . $$ The third term is the moment of inertia around the center of mass ($I_0$) and $\omega$ is the rotational speed around the center of mass in the center of mass frame.

Both the second and third terms are considered rotational kinetic energy, but only the third is invariant under changes of reference frame. Consider, for example, if the center of mass is moving along the radial direction (or instantaneously at the origin), then the second term is $0$. Just shift the origin to a different position, though, and the second term has rotational kinetic energy.

This is actually closely related to the parallel axis theorem, where $$I_{\mathrm{tot}} = m r_{\mathrm{CM}}^2 + I_0.$$

Another way to see this is to write the kinetic energy in terms of angular momentum, which is different depending on which origin you choose, but is conserved by inertial motion: $$K = \frac{1}{2}m\dot{r}_{\mathrm{CM}}^2 + \frac{L_{\mathrm{CM}}^2}{2 m r_{\mathrm{CM}}^2} + \frac{1}{2} I_0 \omega^2.$$ For inertial motion the path followed is given by: \begin{align} \vec{r} & = (x_0 + v_x t)\hat{i} + (y_0 + v_y t)\hat{j} \Rightarrow \\ r & = \sqrt{\left(x_0 + v_x t\right)^2 + \left(y_0 + v_y t\right)^2} \\ \theta & = \operatorname{atan2}\left(y_0 + v_y t, x_0 + v_x t\right). \end{align} Since $L_{\mathrm{CM}}$ is a constant, the second term goes to zero like $t^{-2}$ for long times - so rotational kinetic energy is not even a constant for the inertial motion of an individual particle, let alone invariant under changes of coordinate system origin.

Answer 2

I think I understand your confusion, but you've got the answer in your own question, just read calm and try to understand.

The torque denotes the "capability" of a force to make the body rotate around the point you chose.

So there is no contradiction. If you choose the one of $r_0$, the force cannot make the ball rotate around that point. However, the force actually CAN make the ball rotate around other point like the one in $r_1$, or $r_2$.

By the way, you can set the reference of torques outside your origin of coordinates. The torque will just be $\vec{r}_{ref-to-object} \times \vec{F}=(\vec{r}_{obj}-\vec{r}_{ref})\times \vec{F}$.

Finally, kinetic energy is not directly related to torque, but $E_k$ does also depend on the reference frame, and that's not a problem.

Answer 3

You can actually prove that the kinetic energy of any system is generally invariant under changing the reference point of your torque and angular momentum. An easy way to see this is by using the relation for kinetic energy in terms of the angular momentum and angular velocity (with some arbitrary reference point): $$E_K = \frac12 \mathbf L . \boldsymbol \omega$$ Now from the definition of the torque with respect to our arbitrary reference point: $$E_K = \frac12 \mathbf L . \boldsymbol \omega =\frac 12 (\sum_i m_i \ \mathbf r_i \times \mathbf v_i ).\boldsymbol \omega =\frac 12 \sum_i m_i \ \boldsymbol \omega.(\mathbf r_i \times \mathbf v_i)=\frac 12 \sum_i m_i \ \mathbf v_i.(\boldsymbol \omega \times\mathbf r_i ) $$ Now since the velocity of the i$^{th}$ particle is $\mathbf v_i = \boldsymbol \omega\times \mathbf r_i$ , we get: $$E_K=\frac 12 \sum_i m_i \ \mathbf v_i.\mathbf v_i = \frac 12 \sum_i m_i |\mathbf v_i|^2 $$ But because the velocities are intrinsically independent of the reference point, $E_K$ must also be independent of the reference point. You can easily extend this argument to continuous systems by changing the sums to integrals.

As you can see the above relation was expected because it's simply the sum of the individual kinetic energies of the constituent particles; which, again, is intrinsically independent of any reference point.

Edit:

As Sean E. Lake points out in his answer, how you divide the total kinetic energy into rotational and non-rotational kinetic energies does depend on the reference point. However, this is not important because as shown in my answer, the total kinetic energy is invariant. Also, the kinetic energy does depend on the reference frame because the two reference frames can have a relative velocity with respect to each other. I have just shown the invariance of the kinetic energy with respect to the reference point, i.e. the two reference frames are stationary with respect to eachother, with just different origins, in my derivation.