To calculate the frequency of some wave source, does the wave source have to emit waves continuously?

Question

I understand that the frequency is the number of waves that pass a place in a given amount of time. And it is shown like this:

But, the frequency of waves are always shown above as if the source of wave (let’s say it is light) is continuously emitting waves. What i mean is, isn’t there a time elapse between the individual pulses of waves.

For example light emitted from an hydrogen atom, the frequency of that light would be shown as above. But when each time the electron of hydrogen atom goes to an higher state and a lower state, i think there must be a time elapse. And if you were not to take that into account, wouldn't you get the wavelength of that wave source longer.

Note: My English language is not very good, so if i made mistakes that made the question harder to understand, I apologise.

Answer 1

Your understanding of what constitutes a 'pulse' is flawed. If you excite an atom, then the emitted radiation will indeed be confined in time, forming a pulse, but this will take the form of a larger envelope that encases the individual oscillations at the resonance frequency.

A typical example looks like this:

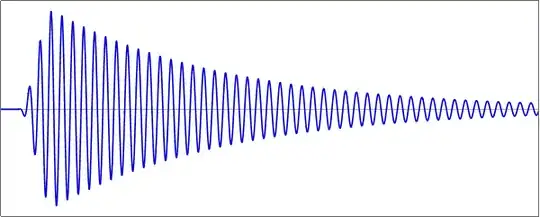
You have an initial ramp-up phase, caused by whatever is bringing the population from the ground to the excited state, followed by an exponential decay as the atom emits its energy as electromagnetic radiation. (Why an exponential? because the Einstein-coefficient formalism tells you that the rate of emission is proportional to the population in the excited state.)

Within that envelope, however, you have individual oscillations of the electromagnetic field, and those are a good map of the charge oscillations within the atom as it winds down. The frequency of the emitted light is (the inverse of) the time between successive maxima of this oscillation.

It is important to note that the diagram above has parameters that are somewhat exaggerated to be able to draw things. For most normal atomic emission lines, the pulse is much longer (compared to the carrier frequency $\omega_0$) than what I've drawn: the pulse envelope decays with a lifetime $\tau$ of a few nanoseconds, whereas the period of the internal oscillations is about a few femtoseconds, i.e. the envelope will typically fit several million oscillations of the carrier. This means that when you're calculating the frequency of the emission, as an initial approximation, you can just forget about the presence of the envelope.

If you do want to include it, however, then the usual approach is to add it as the imaginary part of the oscillation frequency: the electric field of the signal can incorporate both the trigonometric oscillations and the exponential decay as a single dependence if you rephrase it as $$ E(t) = \mathrm{Re}\bigg[E_0 e^{-i\left(\omega_0 -\frac{i}{\tau}\right)t}\bigg], $$ with a single complex frequency $\omega = \omega_0 -i/\tau$. However, that's probably too technical for you at this stage: for all intents and purposes, you just calculate the frequency by looking at the internals of the pulse, but if you do want to include the envelope, then this is how you do it.

Now, in many experiments you will excite the atom, look at the radiation, then wait a bit, and then re-excite it to produce a second pulse of radiation, wait some more, re-excite, and so on. This will then produce a train of pulses, but their separation is not called their frequency - it is called the repetition rate of the source.