Parametric equation for the electric field of a uniformly charged surface with a triadic Koch curve fractal perimeter

Question

I'm currently studying fractals as well as electrodynamics. So, I thought why not create a problem using concepts from both subjects.

I want to study the electric field, at the centroid of the initial triangle, of a charge $q$ that's uniformly distributed across the n-th iteration of a triadic Koch curve. This would be a rather lengthy problem, but be solvable by using self-similarity and symmetry of the Koch curve.

Edit : From the symmetry of the problem, the field would be zero for sure.

But this problem becomes invalid for the $\infty$-th iteration of the triadic Koch curve, as an infinite amount of charge would be needed to fill the perimeter.

But what if we think of a surface uniformly distributed charge, whose perimeter is the $\infty$-th iteration of a triadic Koch curve (no charge on the perimeter :) ), for which I want to calculate the electric field at some perpendicular distance $d$ from the centroid. How can the parametric equation be worked out in this case?

I just want some hints, as I don't know how to attack the problem.

Answer 1

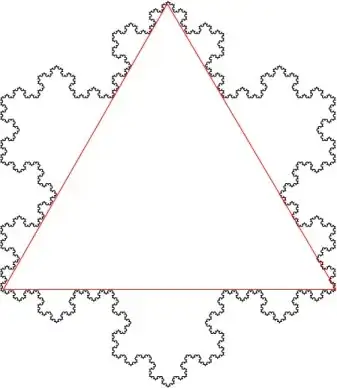
Here are a few observations about this problem:

1) You mention that an infinite amount of charge would be needed by the $\infty$-th iteration, but this is not so. By holding the amount of charge in the system constant, the linear charge density of the shape can easily be determined to be

$$ \lambda_n=\frac{3^{n-1}Q}{4^nL} $$

where $Q$ is the total charge and $L$ is the length of one side of the initial equilateral triangle. This means that the linear charge density of the $0$-th iteration (the triangle) is $\frac{Q}{3L}$ as expected.

2) However, your observation that the problem becomes invalid in the fractal limit (at the $\infty$-th iteration) is correct. It becomes invalid not due to an infinite amount of charge but because the curve is no longer integrable. A fractal has an uncountable number of discontinuities and is therefore not differentiable - which is a requirement for computing the integral that determines the field of this shape.

3) That integral for the electrostatic potential can be stated quite briefly as

$$ \phi(\vec x)=k \lambda_n\int_{C}\frac{dl}{|\vec x -\vec x_0|} $$

where $\phi (\vec x)$ is the electrostatic potential at point $\vec x$ in space, $k$ is Coulomb's Constant, $\lambda_n$ is the charge density defined above, $C$ is the curve defined by the perimeter of the Koch Snowflake, $dl$ is the infinitesimal length along $C$, and $\vec x_0$ is the location in space of that infinitesimal length.

Long story short, you can parameterize the curve (and therefore $dl$) over $\vec x_0$ and take the integral. Because of the symmetry, you'd only need to complete the integral for one side of the snowflake and then multiply by 3. This process is possible (albeit cumbersome and tedious) for all finite n; however, taking the limit will fail since the curve has no infinitesimal smoothness.

That said, with enough time, you could write a computer program that correctly paramaterizes the curve and computes the integral for any value of n. If you did this (which is by no means a trivial task), you ought to find that the integral's result for higher and higher values of n slowly converges. So, in a way, you can determine the limit through numerical approximation, but this process would be very challenging and has no corresponding functional limit.

4) A similar argument can be made for your reframed question. All you would do is construct a surface charge density and do a 2-dimensional integral over the area of the shape. This integral is no easier than the other one, but I would expect it to also slowly converge.

Answer 2

This is a beautiful problem, it's one of my favorites on the site, although seems to me more mathematics-wise challenging than physics-wise. I appreciate especially its symmetry and recursive-like touch, but a mathematitian might have an analytical method to solve it, you should post it on MSE.

I will only outline my solution, as you request, but if you want it more explicit I can add more details. I will also write a routine to calculate it approximately, and share it over here too. Here is my approach:

Summary of solution

The Koch surface can be constructed by successive additions of triangles. The superposition principle justifies finding the total Electric field of the surface as the addition of the electric field produced by each the triangles added.

Solution methodology

Initial simplifications

The Koch surface has a finite area which is $\frac{8}{5}$ of the initial triangle $a_o$, and the uniform charge density would be $\sigma=\frac{5q_o}{8a_o}$ being $q_o$ the total charge. Each triangle added will have the same density, and of course, a charge proportional to its area.

The construction of the area by addition of triangles, distributes them always with polar symmetry in relation to the centroid. This means that components of the electric field of each iteration are cancelled out, and only the components perpendicular to the plane (along the direction of $d$) contribute to the total electrical field. In other words, the electric field of a Koch surface above the centroid is oriented parallel to the perpendicular to the surface, since it has polar symmetry around this point.

---

Method

At each iteration, a number of equilateral triangles $N_n$ of side length $s_n$ is added at positions from the centroid $\{ {\bf r}^k_n, k \in [1, N_n] \}$ (with modulus $\{ r^k_n, k \in [1, N_n] \}$) and orientations $\{ \alpha^k_n, k \in [1, N_n] \}$. The contribution of each triangle to the electric field is: $$E_n = \sum_{k=1}^{N_n}{\rm E}(d, s_n, \alpha^k_n, {\bf r}^k_n)$$ Thus the total electric field will be: $$E = \sum_{n=1}^{\infty}E_n$$

Let's determine each of the elements needed.

• $N_n = 3\times 4^{n-1}$
• $s_n = \frac{s_o}{9^n}$ where $s_o$ is the side length of the initial triangle
• ${\bf r}_n^k$ can be found recursively, by means of the previous ones ${\bf r}_{n-1}^k$. Let's define that ${\bf r}_n^k$ will always point to the centers of each of the sides in the current iteration. The vector in the previous iteration ${\bf r}_{n-1}^k$ was pointing to the center of some side. The new triangle placed there (with a side length 1/3 of the previous side size) introduces 4 new sides. Their centers can be found as: ${\bf r}_n^{k_i} = {\bf r}_{n-1}^k + \Delta {\bf r}_{n-1}^i$ where $\Delta {\bf r}_{n-1}^i$ have 4 different values: $-\frac{s_{n-1}}{3}{\hat h}^k_{n-1}$, $\frac{s_{n-1}}{3}{\hat h}^k_{n-1}$, $\frac{s_{n-1}}{12}\left( -{\hat h}^k_{n-1}+\sqrt{3}{\hat o}^k_{n-1}\right)$, $\frac{s_{n-1}}{12}\left( {\hat h}^k_{n-1}+\sqrt{3}{\hat o}^k_{n-1}\right)$ where ${\hat h}^k_{n-1}$ and ${\hat o}^k_{n-1}$ are versors respectively along and perpendicular to the direction of the $k$th side in the $n-1$th iteration.
• $\alpha_n^k$ can be determined also recursively, I prefer to use the angle between ${\bf r}_n^k$ and ${\hat o}^k_{n-1}$, but a different one can be used, as long as the function below is calculated correctly as a function of $\alpha_n^k$
• ${\rm E}(d, s_n, \alpha^k_n, {\bf r}^k_n)$ is the component along the vertical on a point above the centroid at height $d$ (see above) of the electrical field from an evenly charged equilateral triangle located at a distance ${\bf r}_n^k$ from the centroid and orientation $\alpha_n^k$: $${\rm E}(d, s_n, \alpha^k_n, {\bf r}^k_n) = k_e\sigma\frac{\sqrt{3}}{4}s^2_n \int\int \frac{dxdy}{|{\bf r}^k_n + {\bf d}|^2}\cos{\phi^k_n}$$ with $\phi^k_n$ being the angle of the distance of the position of the triangle (center of the $k$th side in the $n-1$th iteration) to the point of interest at $d$ from the plane $$\cos{\phi^k_n} = \frac{d}{|{\bf r}^k_n + {\bf d}|}$$

Answer 3

I think this problem might be solvable using differential chains https://arxiv.org/abs/1210.4528

They are are a mathematical structure that is effectively a predual to differential forms, meaning they formalize and extend the notion of "domain of integration". It is not hard to represent self-similar fractals as differential chains (see fig. 2) and their limit does exist in many interesting cases. This would allow you to (at least formally) integrate over the $n\to \infty$ limit of the Koch snowflake, and be confident that your limit actually converges in a meaningful sense.

It is likely possible to port the differential form formalism of electromagnetism to differential chain language and solve the problem on your funky domain over there. It is not an easy task, but seems tractable.