How do electromagnetic waves wave?

Question

Electromagnetic waves have a physical crest and trough as observed in microwaves and radio waves. I understand that is electromagnetic field vectors that wave, not the photon. But how do they wave? What does causes them to change direction?

Answer 1

Photon's only move in their direction of travel, it is the electric field vector and magnetic field vector that oscillate, making them waves.

The presence of these fields induces fields in adjoining space, thus the energy in the field travels, wave like.

Answer 2

For microwave ovens, it is not useful to try to analyze the heating process in terms of photons and electrons. This process is understood as AC electric fields acting on water molecules with an electric dipole moment. An electric field will polarize water (the relative permittivity of the liquid is about 80), doing work on the molecules. When the field is turned off, the orientation of the molecules will relax to randomness again. So energy is transformed to heat.

The more often this happens, the higher the rate of heating. In a household microwave oven this is done $2.45\cdot10^9$ times per second, but the exact frequency is not important.

Answer 3

It is important to remember that an electromagnetic wave is exactly what it says on the tin: an electro-magnetic wave, i.e. it contains both an oscillating electric and an oscillating magnetic field.

When the amplitude of one of the fields decreases, it causes also a change in the other field, and vice versa. This is due to Maxwell's equations, which link the changes of electric and magnetic fields in time and space.

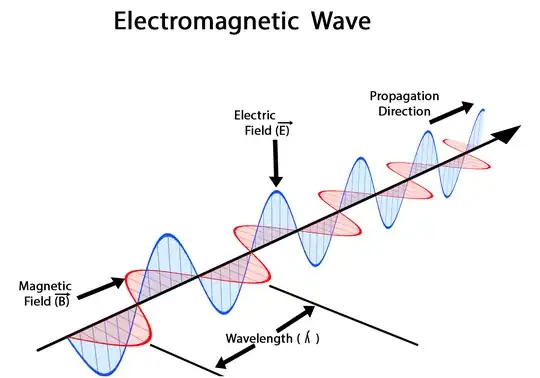
A helpful picture to visualize what is going on in such a wave is the following:

As you can see, the electric field alone propagates as a sine wave, as does the magnetic field. However, it matters that they are both propagating along the same direction and have the same phase, while their polarization (the direction their field vectors point in) are 90° offset.

Maxwell's equations specifically state that a change in space of the electric field ($\nabla \times \vec E$) causes a change in time in the magnetic field ($- \frac{\partial \vec B}{\partial t}$). The second equation goes the other way around: a change in space in the magnetic field ($\nabla \times \vec B$) causes a change in time in the electric field ($\frac{1}{c^2} \frac{\partial \vec E}{\partial t}$).